Разработка и исследование метода решения двухкритериальной задачи о рюкзаке применительно к распределению информационных и материальных ресурсов

На правах рукописи

ЗАМКОВА Любовь Ивановна

РАЗРАБОТКА И ИССЛЕДОВАНИЕ

МЕТОДА РЕШЕНИЯ

ДВУХКРИТЕРИАЛЬНОЙ ЗАДАЧИ О РЮКЗАКЕ

ПРИМЕНИТЕЛЬНО К РАСПРЕДЕЛЕНИЮ ИНФОРМАЦИОННЫХ И МАТЕРИАЛЬНЫХ РЕСУРСОВ

Специальность:

05.13.17 «Теоретические основы информатики»

АВТОРЕФЕРАТ

диссертации на соискание ученой степени

кандидата технических наук

Таганрог - 2010

Работа выполнена в Технологическом институте Федерального государственного автономного образовательного учреждения высшего профессионального образования «Южный федеральный университет»

Научный руководитель: доктор технических наук, профессор

Чефранов Александр Георгиевич

Официальные оппоненты: доктор технических наук

Ромм Яков Евсеевич.

доктор технических наук, профессор

Першин Иван Митрофанович.

Ведущая организация: Федеральное государственное унитарное предприятие «Таганрогский научно-исследовательский институт связи»

Защита диссертации состоится «   18      »   февраля     2011 г. в 1420 на заседании диссертационного совета Д.212.208.21 при Южном федеральном университете по адресу: 347928, г. Таганрог, пер. Некрасовский, 44, ауд. Д-406.

С диссертацией можно ознакомиться в зональной научной библиотеке ЮФУ по адресу: г. Ростов-на-Дону, ул. Пушкинская, 148.

Автореферат разослан « 30 » декабря 2010 г.

Просим Вас прислать отзыв на автореферат, заверенный гербовой печатью учреждения, по адресу: 347928, ГСП -17А, Ростовская область, г. Таганрог, пер. Некрасовский, 44, диссертационный совет Д 212.208.21.

Ученый секретарь

диссертационного совета

доктор технических наук, профессор

Н.И. Чернов

ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ

Актуальность.Рациональное расходование материальных и информационных ресурсов является важной научно-технической и практической задачей. Рациональное расходование ресурсов неразрывно связано с эффективным использованием финансовых затрат. В связи с этим классические постановки практических задач пересматриваются и возникают новые, в которых учитывается эта составляющая. Прототипом практических задач расходования материальных и информационных ресурсов, которые рассматриваются в диссертационной работе, являются известные классические задачи. В постановке известной задачи загрузки одного процессора целевая функция определяется как среднее время обслуживания работ. В формулировке задачи одного станка в качестве целевой функции используется время обработки деталей. Поиском приложений задачи Джонсона (задачи о станках) продолжают заниматься в настоящее время. В классической постановке задачи раскроя материалов критерием оптимизации является количество комплектов. В диссертации рассматривается ряд двухкритериальных задач, прототипами которых являются указанные однокритериальные. В качестве критериев решения задачи оптимальной загрузки контейнера определяется суммарная стоимость погрузки и суммарный вес предметов. Оптимальная загрузка станка предполагает максимизацию прибыли от реализации деталей и минимизацию времени изготовления деталей. Первый критерий при оптимальном раскрое материала – площадь остатка листа, а второй – количество разрезов (что приводит к экономии энергии). Точно также оптимальное сохранение файлов предполагает максимизацию суммарного объёма и максимизацию количества сохраняемых файлов. Во всех этих задачах предусматривается рациональное расходование материальных и информационных ресурсов (стройматериала, памяти информационного носителя, грузоподъёмности автотранспортного средства). Эта информация задаётся в виде ограничения в постановках рассмотренных задач. В рассмотренных двухкритериальных задачах первый критерий является главным, а второй второстепенным, но в совокупности они описывают одну оптимизационную задачу и являются неразделимыми. Таким образом, эти задачи можно отнести к классу лексикографических многокритериальных задач.

В настоящее время существует два основных подхода к решению этого класса задач:

• последовательная оптимизация;
• скаляризация векторного критерия.

Первыйподходпредполагает разбиение многокритериальной задачи на последовательность взаимосвязанных однокритериальных задач и их решение.

Второйподход предполагает нормализацию частных критериев в составе векторного, и далее построение суперкритерия, агрегирующего частные критерии исходной многокритериальной задачи. В рамках подходов существуют методы решения: метод последовательных уступок и метод свёртки в агрегированный критерий. Процедура решения многокритериальной задачи методом последовательных уступокзаключается в том, что все частные критерии располагают и нумеруют в порядке их относительной важности; максимизируют первый, наиболее важный критерий; затем назначают величину допустимого снижения значения этого критерия и максимизируют второй по важности частный критерий при условии, что значение первого критерия не должно отличаться от максимального более чем на величину установленного снижения; снова назначают величину уступки, но уже по второму критерию и находят максимум третьего по важности критерия при условии, чтобы значения первых двух критериев не отличались от ранее найденных максимальных значений больше чем на величины соответствующих уступок; далее поочередно используются все остальные частные критерии; оптимальной обычно считают любую стратегию, которая получена при решении задачи отыскания условного максимума последнего по важности критерия. Таким образом, при использовании метода последовательных уступок многокритериальная задача сводится к поочередной максимизации частных критериев и выбору величин уступок. Величины уступок характеризуют отклонение приоритета одних частных критериев перед другими: чем уступки меньше, тем приоритет жестче. Одним из распространенных методов решения многокритериальных задач является метод сведения многокритериальной задачи к однокритериальной путем свертывания векторного критерия в суперкритерий. При этом каждый критерий умножается на соответствующий ему весовой коэффициент (коэффициент важности). Здесь возникают трудности с правильным подбором весовых коэффициентов.

Перечисленные методы применяются к общей постановке лексикографической многокритериальной задачи. Целесообразно выделить из этого класса задачу, которая является моделью рассмотренных практических двухкритериальных задач. Формулирование частной постановки задачи, принадлежащей указанному классу, даёт возможность решать её известными общими методами, но остаётся актуальной разработка нового эффективного метода решения именно этих практических задач.

Это направление является актуальным. Существует ряд двухкритериальных лексикографических задач, которые были сформулированы на современном этапе, например:

• при разработке методов решения вершинного варианта задачи анализа уязвимости сетевых систем была сформулирована задача анализа уязвимости многопродуктовой сети с учетом выхода из строя полностью одной или нескольких вершин, которая формализована в виде двухкритериальной лексикографической задачи оптимизации;

• при оптимизации инвестиционного портфеля страховщика требуется найти такую структуру портфеля, для которой ожидаемая доходность максимальна, а совокупный риск минимален, то есть возникает формальная двухкритериальная постановка.

Недостатком метода последовательных уступок является то, что в итоге поиск решения однокритериальных задач базируется на симплекс-методе, который относится к классу экспоненциальных. Это приводит к существенным временным затратам. Недостатком метода свёртки в функционал является то, что при решении итоговой однокритериальной задачи многократно используется один и тот же метод, что также ведёт к увеличению затрат времени на поиск решения. Для разработки метода решения частной двухкритериальной постановки целесообразно выбрать подход расширения линейного пространства, которое включает область допустимых решений. При этом подходе за счёт отсечений достигается уменьшение количества перебираемых решений. Совершенствованием и разработкой методов решения оптимизационных задач различных классов занимались Брахман Т.Р., Данциг Д., Заславский А.А., Куо Б., Карелин В.П., Констанденко О.С., Лебедев Б.К., Ногин В.Д., Пападимитриу Х., Подиновский В.В., Стайглиц К., Табак Д. и др.

Среди актуальных приложений лексикографической многокритериальной задачи можно выделить несколько наиболее перспективных:

• применение для нахождения эффективных управлений при исследовании динамики продольного движения пучка заряженных частиц в ускорителе на бегущей волне;
• управления ассортиментной политикой предприятий оптовой торговли;
• расчёта показателей эффективности технологической системы производства гибридных интегральных схем;
• оценки эффективности информационных систем с использованием технологии открытых систем (сетевой среды филиала банка);
• анализа технологичности карт раскроя материалов при производстве мебели.

Таким образом, на практике было выявлено существование ряда задач, которые требуют более эффективных решений, например, задача загрузки контейнера, задача сохранения файлов на внешний носитель информации, задача раскроя материала и так далее. Формулирование оптимизационной модели этих практических задач, дает возможность разработки эффективного метода для поиска наилучшего оптимального решения.

В диссертационной работе рассматривается булева двухкритериальная задача о рюкзаке. Применительно к практическим задачам, указанным ранее, ее можно классифицировать как информационную модель. Действительно, два входных вектора R=(ri) и L=(li), i=1,2,…,z, которые на практике несут определенную информацию о моделируемом явлении, преобразуются в выходной вектор y* (оптимальное решение двухкритериальной задачи о рюкзаке). Преобразование задается как оптимизационная двухкритериальная задача о рюкзаке (система линейных критериев и ограничение).

Поиск оптимального решения дает возможность эффективно расходовать ресурс при каждом практическом применении (например, финансы, стройматериал, память информационного носителя). Таким образом, разработка информационной модели, булевой двухкритериальной задачи о рюкзаке, является актуальной.

Целью диссертационной работы является постановка двухкритериальной задачи из класса лексикографических многокритериальных задач (видоизменение задачи о рюкзаке) применительно к расходованию материальных и информационных ресурсов, разработка и исследование эффективного метода ее решения.

Для достижения цели диссертационной работы необходимо:

• сформулировать постановку двухкритериальной задачи из класса лексикографических многокритериальных задач (видоизменение задачи о рюкзаке) применительно к расходованию материальных и информационных ресурсов;
• разработать алгоритм решения поставленной задачи;
• исследовать временную сложность предложенного алгоритма решения данной задачи в сравнении с известными методами решения задач рассматриваемого класса;
• оценить эффективность разработанного алгоритма в практическом аспекте.

Методы исследования.

В диссертационной работе применялись элементы теории вероятностей, математической статистики, теории графов, линейной алгебры, методы математического программирования.

Научная новизна. Научная новизна диссертационной работы заключается в следующем:

1. Разработан метод решения булевой двухкритериальной задачи о рюкзаке, основанный на частичном переборе допустимых решений путём расширения линейного пространства допустимых решений. Метод по построению отличается от известных методов класса многокритериальных лексикографических задач, обладает преимуществом в эффективности и позволяет снизить временную сложность решения задачи о рюкзаке.
2. Сформулировано и обосновано положение о независимости решения двухкритериальной задачи о рюкзаке от перестановки числовых коэффициентов, определяемых при её постановке. Положение отличается от аналогов в данном классе задач и на практике позволяет оптимизировать расход материальных и информационных ресурсов.
3. Для решения двухкритериальной задачи о рюкзаке адаптированы метод свертывания в агрегированный критерий, выведены формулы расчёта числовых коэффициентов. Получено отличное от известных в данном классе задач формальное описание метода решения рассматриваемой задачи, что позволило представить программную реализацию решения.
4. На основе сравнения временной сложности предложенного метода, метода последовательных уступок, а также свертывания в агрегированный критерий показано, что предложенный метод решает двухкритериальную задачу о рюкзаке вдвое быстрее метода последовательных уступок и в пять раз быстрее свертывания в агрегированный критерий.

Достоверность результатов вытекает из их математического обоснования, подтверждается статистическими оценками, иллюстрируется результатами работы комплекса программ.

Основные положения, выносимые на защиту.

1. Метод решения двухкритериальной задачи о рюкзаке, основанный на частичном переборе допустимых решений путём расширения линейного пространства допустимых решений.
2. Положение о независимости решения рассматриваемой двухкритериальной задачи от перестановки числовых коэффициентов, определяемых при её постановке.
3. Адаптированный метод свертывания в агрегированный критерий для решения двухкритериальной задачи о рюкзаке, формулы расчёта числовых коэффициентов.
4. Сравнительные оценки временной сложности предложенного метода, метода последовательных уступок и свертывания в агрегированный критерий, согласно которым предложенный метод решает рассматриваемую задачу вдвое быстрее первого и в пять раз быстрее второго.

Практическая ценность.

Программный продукт, разработанный на основе предложенного метода оптимизации, может найти применение на предприятиях, занимающихся грузоперевозками, его использование, примерно, на порядок повышает эффективность загрузки по сравнению с загрузкой предметов, отсортированных по весу.

Полученные в работе результаты использованы в ООО «МиР» (Ростов-на-Дону), приняты для загрузки автотранспорта при перевозке стройматериалов; в ЗАО ПКФ «Гефест ВПР» (Таганрог) для изготовления комплектующих при производстве металлоконструкций, что подтверждено соответствующими актами об использовании, приведенными в приложении 8 к диссертационной работе.

Апробация работы. Основные результаты диссертационной работы докладывались на:

• Отраслевой научно-технической конференции “Актуальные проблемы развития железнодорожного транспорта и роль молодых ученых в их решении” (г. Ростов-на-Дону, 1998 г.);
• Всероссийской научной конференции “Новые информационные технологии. Разработка и аспекты применения” (г. Таганрог, 2000 г.);
• Международной научно-технической конференции “Математические методы в экономике” (г. Пенза, 2002 г.);
• 53научно-технической конференции профессорско-преподавательского состава, аспирантов и сотрудников Технологического института Южного федерального университета в г. Таганроге (2008 г.).

Основные результаты опубликованы в 7 печатных работах, из них 2 работы в изданиях, входящих в перечень ведущих научных журналов и изданий, выпускаемых в Российской Федерации, утверждённый ВАК.

Объем и структура работы. Диссертационная работа состоит из введения, четырех глав, заключения, списка литературы, включающего 96 наименований, и 8 приложений. Работа изложена на 119 стр., включает 85 стр. приложений, содержит 9 рисунков и 8 таблиц.

СОДЕРЖАНИЕ РАБОТЫ

В первой главе “Двухкритериальная задача о рюкзаке и методы многокритериальной оптимизации” формулируется постановка булевой двухкритериальной задачи о рюкзаке:

(1)

Эта задача является моделью следующих практических задач: оптимальной загрузки станка, оптимальной загрузки контейнера, оптимизации раскроя материала, оптимального сохранения файлов на носителе информации. Так как эта задача принадлежит классу многокритериальных лексикографических задач оптимизации, в этой главе приводится описание методов решения задач этого класса: метода последовательных уступок и метода свертывания в агрегированный критерий.

В основу метода последовательных уступок положена последовательная оптимизация, то есть исходная многокритериальная задача разбивается на последовательно решаемые однокритериальные задачи.

Метод свертывания в агрегированный критерий базируется на принципе скаляризации многокритериальных задач. Этот метод предполагает построение линейного функционала из частных критериев исходной многокритериальной задачи, путем введения весовых коэффициентов для каждого критерия. Таким образом, многокритериальная задача сводится к однокритериальной. Далее в этой главе рассматриваются методы решения однокритериальных задач, которые используются в диссертационной работе.

Во второй главе “Разработка метода двойной оптимизации решения двухкритериальной задачи о рюкзаке” разрабатывается метод двойной оптимизации решения двухкритериальной задачи о рюкзаке. Метод двойной оптимизации (МДО) отличается от методов своего класса подходом к поиску решения. Основными, известными подходами при решении двухкритериальной задачи о рюкзаке являются линеаризация и последовательная оптимизация. Метод двойной оптимизации действует в рамках подхода расширения пространства, которому принадлежит область допустимых решений исходной задачи. При разработке метода двойной оптимизации предложен новый механизм перебора решений, который приводит к оптимальному решению двухкритериальной задачи о рюкзаке.

Применение переборных методов на практике возможно только при наличии механизма перебора, то есть это ключевой момент в переборных методах.

Поиск оптимального решения задачи (1) методом двойной оптимизации сводится к построению допустимых решений z задач вида:

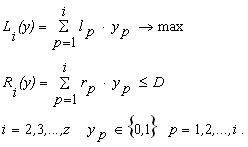(2)

Множество C1 всегда содержит два вектора (0) и (1).

Для задачи размерности i строится множество допустимых решений Ci. Элементы Ci упорядочиваются по возрастанию целевой функции. Множество Ci, i=2,3,…,z формируется на основе множества Ci-1.

Для каждого вектора , где j=1,2,...,|Ci-1|, проверяются последующие условия. Если |Ci|=0, то вектор помещается на первое место в Ci. Если в Ci нет векторов, дающих равное или большее значение целевой функции чем , то вектор помещается на последнее место в Ci.

Если в Ci есть вектор , где j1=1,2,…,|Ci|, со значением целевой функции, равным значению целевой функции от вектора , то анализируется условие . При истинности этого условия вектор считается доминирующем над вектором и помещается в Ci на его место, а вектор отсекается. При ложном значении множество Ci не изменяется.

Если в Ci есть вектор , дающий большее значение целевой функции чем , то заносится перед таким вектором. Если , то вектор заносится в Ci на последнее место. Вектора и являются потомками размерности i вектора .

Сформированное таким образом множество Сi содержит векторы, упорядоченные по возрастанию значений целевой функции. Результатом работы метода двойной оптимизации является вектор opt, который расположен в Сz на последней позиции.

Идея расширения размерности векторов в процессе перебора при поиске оптимального решения реализована в методе последовательного анализа вариантов. Но проблема заключается в том, чтобы задать механизм перебора. Различие переборных методов заключается именно в механизме перебора. В методе последовательного анализа вариантов из источника, приведённого в диссертации, описана идея переборного метода, но не задан механизм перебора, что делает невозможным применение любого переборного метода на практике. В методе двойной оптимизации разработан механизм перебора решений, который не допускает потери оптимального решения. Это доказывается в обосновании метода.

Далее в главе на основании концептуального описания метода приводится псевдокод программы. Рассматривается на конкретных примерах функционирование метода двойной оптимизации.

Приводится обоснование метода двойной оптимизации. В основе метода двойной оптимизации заложено построение множеств решений двухкритериальной задачи о рюкзаке, которые упорядочиваются по возрастанию значений первого критерия. Доказывается, что на одном порядке коэффициентов булевой двухкритериальной задаче о рюкзаке метод двойной оптимизации приводит к оптимальному решению y*. Далее выдвигается гипотеза о том, что при любом упорядочивании коэффициентов в булевой двухкритериальной задаче о рюкзаке метод двойной оптимизации приводит к такой же выборке коэффициентов, которая соответствует y*. Проводится анализ решений, выдаваемых методом двойной оптимизации, при различных упорядочиваниях. В качестве аналога сравнения результатов берется оптимальное решение y*. В итоге анализа не находится опровержения гипотезы.

В процессе доказательства того, что на одной перестановке коэффициентов задачи (1) МДО приводит к оптимальному решению y*, формулируется утверждение 1 и утверждение 2.

Утверждение 1. Решение, отбрасываемое по превышению D в процессе вычисления методом двойной оптимизации, не может привести к оптимальному решению задачи (1).

Утверждение2.Отсечениевекторапоусловию доминирования не приводит к потере оптимального решения задачи (1).

Далее представим идею доказательства утверждения 1. Если решение является недопустимым (то есть значение функции R превышает D), то оно исключается из множества перебираемых решений. По построению множеств Ci, i=2,3,…,z (решений-векторов размерности i) потомок размерности i+1 недопустимого решения может иметь значение функции R равное или большее, чем вектор его породивший. Таким образом, значение функции R от потомка тем более превышает D, то есть этот потомок является недопустимым решением. Это справедливо для всех потомков размерности i+1, i+2, …, z. Таким образом, все потомки являются недопустимыми решениями.

Представим идею доказательства утверждения 2. Рассмотрим два произвольных вектора и , для которых выполняется условие доминирования и . Дерево G всех потомков вектора будем называть идентичным дереву V всех потомков вектора . На дереве V, вершины которого участвуют в переборе, выделяется подграф: вершина и два её потомка и . Рассматриваются ситуации включения или исключения из перебора векторов и . Обосновывается, что соответствующие потомки и на G, не будут являться доминирующими векторами. Эти рассуждения применяем к каждой вершине-вектору размерности k+1, k+2, …, z-1 на дереве V. То есть отсечениевекторапоусловию доминирования не приводит к потере оптимального решения.

Далее в этой главе была сформулирована гипотеза для обоснования оптимальности МДО.

ГИПОТЕЗА. Предполагается, что значение критериев от вектора-решения задачи (1), определяемого методом МДО, не зависит от перестановки коэффициентов в критериях.

Для обоснования гипотезы проводилось 1000 запусков программы на базе МДО. Запуски производились на различных произвольных перестановках исходных коэффициентов, которые соответствовали 50 индивидуальным задачам (1). Для каждой перестановки, соответствующей одной задаче, итоговые значения критериев, соответствующие решению задачи, совпали, что выполнилось для каждой задачи.

В третьей главе “Сравнительный анализ метода двойной оптимизации с методом последовательных уступок и методом свертывания в агрегированный критерий” разрабатываются алгоритмические реализации метода последовательных уступок (МПУ) и метода свертывания в агрегированный критерий (МСАК). На основании этих алгоритмов, заложенных в программы, проводится сравнительный анализ по времени решения задач вышеуказанных методов. Для 50 индивидуальных задач вида (1), коэффициенты которых генерировались случайным образом, производились опыты. Для серии из 50 опытов рассчитывались оценки математического ожидания и среднеквадратичного отклонения, которые приведены в табл.1.

Табл. 1

	МДО	МСАК	МПУ
M*, секунды	0,109980	0,500080	0,239720
*, секунды	0,006198	0,079317	0,014193

Из табл.1 следует, что величины оценок среднеквадратичного отклонения незначительны, поэтому сравнение методов проводилось по оценкам математического ожидания. В результате определяется то, что метод двойной оптимизации– самый эффективный в своем классе методов, второй по скорости решения– метод последовательных уступок и самый медленный– метод свертывания в агрегированный критерий.

Оценивается быстродействие метода двойной оптимизации при решении двухкритериальных задач о рюкзаке размерности 80, то есть решаемых на практике. Рассматривались задачи, для которых D=2000, 2500, 3000 и z=20,40,60,80. Результаты приведены на графиках рис.1. Согласно графикам рост размерности задач приводит к росту времени их решения методом МДО. Среднее время решения задач на заданном диапазоне является приемлемым, при росте размерности в четыре раза среднее время решения увеличилось в шесть раз.

Рис.1

В этой главе проведена адаптация МСАК для решения задачи (1). Она заключалась в следующем: для поиска весов линейного функционала необходимо решить задачу (3)

(3)

Задача (3) сводится к решению задач вида (4):

, (4)

-оптимальное значение целевой функции задачи

.

Пусть оптимальное решение однокритериальной задачи о рюкзаке при ограничении на вес di. Задача с ограничением на вес D имеет самую большую разность между максимальным и минимальным значением целевой функции L (минимальное значение равно 0). Уменьшая вес рюкзака, и решая полученную задачу, мы находим ближайший максимум к максимуму задачи с предыдущим значением веса. Разность между ближайшим максимумом и минимальным нулевым значением целевой функции будет меньше аналогичной разности для задачи с предыдущим весом. Продолжая подобные рассуждения, мы находим самый ближайший максимум к минимуму. Разность между ними и будет решением задачи (4).

Таким образом, задача, описанная формулой (4), сводится к решению однокритериальных задач о рюкзаке вида (5):

(5)

где -оптимальное значение целевой функции задачи

.

В четвертой главе “Применение двухкритериальной задачи о рюкзаке” рассматривается двухкритериальная задача о рюкзаке в качестве моделей следующих практических задач: оптимальной загрузки контейнера, оптимизации раскроя материала, оптимального сохранения файлов на носитель информации.

В случае применения двухкритериальной задачи о рюкзаке для оптимальной загрузки контейнера в качестве главного критерия определяется стоимость загрузки контейнера, а вторым критерием является общий вес загруженных предметов. Для оптимальной загрузки контейнера рассчитана сравнительная экономическая эффективность согласно маркетинговому подходу. Оптимальная загрузка контейнера в 9 раз эффективнее традиционного порядка выбора предметов для загрузки в контейнер. В итоге расчетов по маркетинговому подходу определяется сравнительная экономическая эффективность по формуле (6):

, (6)

где IЭ интегральный экономический показатель, который определяется по формуле (7):

, (7)

где b1, b2 значения первого и второго параметров соответственно; a1, a2 весовые коэффициенты первого и второго параметров соответственно. Значения параметров аналога и разработки представляют в относительных единицах, то есть всем значениям параметров аналога присваивается значение равное единице, а значениям разработки соответствующее численное улучшение (увеличение) параметра в разах (значение больше единицы) либо соответствующее численное ухудшение (уменьшение) параметра в разах (значение меньше единицы, но больше нуля). Численное значение весовых коэффициентов должно лежать в интервале от 0 до 1, а их сумма равняться единице. Присвоение численного значения весовым коэффициентам осуществляется с позиции их значимости.

В случае применения двухкритериальной задачи о рюкзаке для оптимального сохранения файлов на носитель информации и оптимального раскроя материала, в постановке указанной задачи коэффициенты первого критерия полагаются равными соответствующим коэффициентам ограничения, а коэффициенты второго критерия равны единицам. Критериями при оптимальном сохранении файлов на носителе информации являются общий объем сохраняемых файлов и их количество. Главным критерием, при оптимальном раскрое материала, является суммарная длина листов-заказов, которые получаются в результате раскроя исходного листа, а качестве второго определяется количеством разрезов исходного листа. Для оптимального сохранения файлов и оптимального раскроя материала рассчитана сравнительная эффективность по маркетинговому подходу. Оптимальное сохранение файлов в 14 раз, а оптимальный раскрой материала в 10 раз эффективнее способа, используемого на практике. Для решения индивидуальных постановок каждой практической задачи приводится описание кодов программ, которые организуют обработку исходной и результирующей информации этих практических задач.

Для практических задач рассчитана средняя сравнительная экономическая эффективность согласно маркетинговому подходу. Решение практических задач оптимально и по среднему значению в 11 раз эффективнее традиционного порядка выбора объектов (деталей, листов, файлов, грузов). Результаты расчётов приведены на рис.2.

Рис.2

ОСНОВНЫЕ РЕЗУЛЬТАТЫ РАБОТЫ

1. Метод решения двухкритериальной задачи о рюкзаке, основанный на частичном переборе допустимых решений путём расширения линейного пространства допустимых решений. Опубликовано в [3-7].
2. Положение о независимости решения рассматриваемой двухкритериальной задачи от перестановки числовых коэффициентов, определяемых при её постановке. Опубликовано в [1].
3. Адаптированный метод свертывания в агрегированный критерий для решения двухкритериальной задачи о рюкзаке, формулы расчёта числовых коэффициентов. Опубликовано в [1].
4. Сравнительные оценки временной сложности предложенного метода, метода последовательных уступок и свертывания в агрегированный критерий, согласно которым предложенный метод решает рассматриваемую задачу вдвое быстрее первого и в пять раз быстрее второго. Предварительные результаты опубликованы в [2], а окончательные в [1].

СПИСОК ПУБЛИКАЦИй ПО ТЕМЕ ДИССЕРТАЦИИ

Публикации в изданиях из "Перечня ведущих рецензируемых научных журналов и изданий, выпускаемых в Российской Федерации", утвержденного ВАК

1. Замкова Л.И. Булева двухкритериальная задача о рюкзаке// Известия ЮФУ. Технические науки.– Таганрог, 2009. – №4. – с.201-204.
2. Замкова Л.И. Сравнительный анализ двухэтапного алгоритма с методом последовательных уступок// Известия ТРТУ. – Таганрог, 2006. – №10. – с.30-32.

Публикации материалов и тезисов конференций, статей в сборниках

3. Замкова Л.И. Метод решения задачи максимизации дохода, сведенной к задаче о рюкзаке// Конф. Актуальные проблемы развития железнодорожного транспорта и роль молодых ученых в их решении. – 1998. – С. 166-167.
4. Замкова Л.И. Разработка программной системы эффективной оплаты счетов// Известия ТРТУ. – Таганрог, 2005. – №6. – с.128-134.
5. Замкова Л.И., Чефранов А.Г. Алгоритм принятия решения об оплате счетов на основе решения задачи о ранце// конф. Новые информационные технологии. Разработка и аспекты применения. – Таганрог, 2000. – С. 40-41.

6. Замкова Л.И. Программная система принятия решения об эффективной оплате счетов// Международная научно-техническая конференция Математические методы в экономике. – Пенза, 2002. – С.135-137.
7. Замкова Л.И. Построение двухкритериальной задачи о рюкзаке, математической модели оплаты счетов, и метод её решения// 53 научно-техническая конференция профессорско-преподавательского состава, аспирантов и сотрудников Технологического института Южного федерального университета в г. Таганроге/ Известия ЮФУ.–Таганрог, –2008. –№1.– С.142.

Личный вклад автора в работе [5], опубликованной в соавторстве – предложен алгоритм решения двухкритериальной задачи о рюкзаке.

Соискатель Л.И. Замкова

Типография Технологического института Федерального государственного автономного образовательного учреждения высшего профессионального образования «Южный федеральный университет», заказ № 390, тираж 100 экз. 2010 г.