Разработка и исследование статистических методов текстурной сегментации полутоновых изображений
На правах рукописи
Патана Елена Игоревна
РАЗРАБОТКА И ИССЛЕДОВАНИЕ СТАТИСТИЧЕСКИХ МЕТОДОВ
ТЕКСТУРНОЙ СЕГМЕНТАЦИИ ПОЛУТОНОВЫХ ИЗОБРАЖЕНИЙ
Специальность 05.13.17 – Теоретические основы информатики
Автореферат
диссертации на соискание ученой степени
кандидата технических наук
Таганрог 2009
Работа выполнена в Таганрогском технологическом институте
Южного федерального университета.
Научный руководитель: доктор физико-математических наук, профессор
Сухинов Александр Иванович.
Официальные оппоненты: доктор технических наук, профессор
Ромм Яков Евсеевич.
кандидат технических наук
Спиридонов Олег Борисович.
Ведущая организация: Северо-Кавказский государственный
технический университет, г. Ставрополь.
Защита диссертации состоится « 18 » декабря 2009 г. в 1420 на заседании диссертационного совета Д.212.208.21 Южного федерального университета по адресу: 347928, г. Таганрог, пер. Некрасовский, 44, ауд. Д-406.
С диссертацией можно ознакомиться в зональной научной библиотеке ЮФУ по адресу: г. Ростов-на-Дону, ул. Пушкинская, 148.
Автореферат разослан « 12 » ноября 2009 г.
Просим Вас прислать отзыв на автореферат, заверенный гербовой печатью учреждения, по адресу: 347928, ГСП -17А, Ростовская область, г. Таганрог, пер. Некрасовский, 44, диссертационный совет Д 212.208.21.
Ученый секретарь
диссертационного совета Д 212.208.21
| доктор технических наук, профессор |  | Чернов Н.И. |
Общая характеристика работы
Актуальность. Широко распространенная практика пиксельной обработки изображений часто оказывается некорректной, поэтому возникает необходимость в более эффективных методах анализа визуальной информации. По этой причине на первый план в алгоритмах обработки изображений ставится проблема учета структурной информации, в этом случае целесообразно применение методов текстурного анализа. Одной из наиболее важных задач анализа текстур является предварительная сегментация, что делает возможным последующую интерпретацию и понимание сцены. Задачей текстурной сегментации занималось большое количество исследователей. Однако многие задачи остались нерешенными или решены не самым оптимальным способом. Не было строго формализовано определение текстуры. Введено большое количество статистических характеристик первого и второго порядка, но не было предпринято попыток построить обобщенный подход к статистическим методам и провести анализ текстурных характеристик. По-прежнему нетривиальными задачами остались определение количества текстур и размера модели марковского случайного поля (МСП) для моделирования изображений. В связи с тем, что решение ряда проблем осталось открытым вопросом, в работе поставлены и решены указанные выше актуальные задачи, а также разработаны модификации методов текстурной сегментации, позволяющие более качественно и быстро выполнять её.
Целью работы является построение методов оценки априорных параметров изображения, позволяющих проводить автоматизированную сегментацию, и разработка модификаций методов текстурной сегментации, на основе которых разделение областей текстурной однородности происходит с высокой степени достоверности, проверяемой на тестовых изображениях Бродаца. Для достижения поставленной цели в диссертационной работе решаются следующие задачи:
1. Предложить детально формализованное определение текстуры.
2. Выполнить статистический анализ текстурных характеристик для метода, основанного на построении матрицы взаимного расположения градаций тона. Провести теоретические исследования указанной матрицы.
3. Разработать алгоритм вычисления количества текстур, присутствующих на изображении.
4. Исследовать модели взаимосвязи пикселей для метода, основанного на использовании МСП, с целью выявления уравнения наиболее точно моделирующего текстуру. Разработать алгоритм оценки порядка модели МСП.
5. Адаптировать метод, основанный на выделении локальных участков стационарности, для работы с двумерными изображениями.
6. На основе синтезированных модификаций методов сегментации разработать программный комплекс, реализующий текстурную сегментацию.
Методы исследования опирались на элементы теории вероятностей и математической статистики, теории нечетких множеств, корреляционного анализа, теории марковских случайных полей, а также методы кластеризации и параметрического оценивания.
Достоверность результатов вытекает из их математического обоснования, подтверждается оценками на основе корреляционного и регрессионного анализа, а также результатами работы программного комплекса, разработанного для проведения текстурной сегментации.
Научная новизна результатов исследования заключается в следующем.
1. Предложено определение текстуры, основанное на положениях теории множеств, теории групп и интегрального исчисления, отличающееся детальной формализацией. Разработан метод определения размера текстурного элемента на основе аддитивной текстурной характеристики, который выделяет элементарную часть текстуры и отличается тем, что позволяет вычислять оптимальные значения текстурных характеристик.
2. Построен обобщенный подход к статистическим методам текстурного анализа первого и второго порядка на основе вычисления интеграла Лебега от разложения функции изображения в ряд Тейлора, что отличается от известных подходов по построению и позволяет выразить любой промежуточный массив для построения текстурных характеристик. Для частного случая переходного массива матрицы взаимного расположения градаций тона предложен способ построения её инвариантов относительно наиболее распространенных углов поворотов изображения. Это обеспечивает повышение качества сегментации по сравнению с известными методами и снижает ошибку первого рода в среднем на 3%, второго – на 4%.
3. Предложен метод статистического анализа текстурных характеристик на основе корреляционного анализа и кластеризации при помощи транзитивного замыкания с целью устранения избыточности количества функционалов, что позволяет сократить вычислительные затраты на 40% по сравнению с известным методом сегментации, использующим десять наиболее употребительных текстурных характеристик. С помощью построения гистограммы распределения текстурных функционалов разработан метод определения количества текстур, присутствующих на изображении, который позволяет проводить автоматизированную сегментацию и отличается от существующих методов тем, что может применяться для произвольных «оконных» алгоритмов получения характеристик.
4. Разработан метод оценки порядка модели МСП, основанный на анализе степени взаимосвязи пикселей, который отличается от известных тем, что позволяет не только определить порядок окрестности МСП, но и прогнозировать тип функциональной зависимости. На основе регрессионного анализа синтезирован алгоритм выбора уравнения взаимосвязи пикселей окрестности, который в отличие от случая линейной зависимости более точно моделирует взаимосвязь пикселей, снижая ошибку сегментации первого рода в среднем на 5%, второго – на 4%.
5. Предложен метод текстурной сегментации на основе поиска точек переключения случайных процессов, который отличается от существующих тем, что для расчета текстурных характеристик используется одномерная подобласть размером N пикселей при вертикальной обработке и M при горизонтальной, что сокращает количество операций пропорционально NM/(N+M) по сравнению с известными методами.
6. Разработан программный комплекс для выполнения текстурной сегментации изображений.
Основные положения, выносимые на защиту.
1. Предложено определение текстуры, основанное на положениях теории множеств, теории групп и интегрального исчисления, а также метод определения размера текстурного элемента на основе аддитивной текстурной характеристики, который выделяет элементарную часть текстуры.
2. Построен обобщенный подход к статистическим методам текстурного анализа первого и второго порядка на основе вычисления интеграла Лебега от разложения функции изображения в ряд Тейлора. Для частного случая переходного массива матрицы взаимного расположения градаций тона предложен способ построения её инвариантов относительно наиболее распространенных углов поворотов изображения.
3. Предложен метод статистического анализа текстурных характеристик на основе корреляционного анализа и кластеризации при помощи транзитивного замыкания с целью устранения избыточности количества функционалов. С помощью построения гистограммы распределения текстурных функционалов разработан метод определения количества текстур, присутствующих на изображении, который позволяет проводить автоматизированную сегментацию.
4. Разработан метод оценки порядка модели МСП, основанный на анализе степени взаимосвязи пикселей. С помощью регрессионного анализа синтезирован алгоритм выбора уравнения взаимосвязи пикселей окрестности.
5. Предложен метод текстурной сегментации на основе поиска точек переключения случайных процессов.
6. Разработан программный комплекс для выполнения текстурной сегментации изображений.
Практическая значимость работы определяется программной реализацией предложенных методов определения априорных параметров изображения (размер модели МСП, количество текстур, присутствующих на изображении), а также модернизацией статистических методов текстурной сегментации. Реализован новый подход к анализу текстур как стационарных участков случайных последовательностей. Создан программный комплекс на языке С++ для ОС Windows, реализующий текстурную сегментацию изображений. Работа комплекса устойчиво дает качественные результаты сегментации. Практические результаты диссертации могут успешно применяться для обработки изображений, полученных в оптическом и радиочастотном диапазонах, а также для обработки ультразвуковых и рентгеновских снимков.
Полученные в диссертационной работе результаты приняты к использованию в ЗАО «ОКБ «РИТМ». На основе текстурного анализа определяются границы перехода состояний испытуемого с целью количественных оценок границ состояний, обладающих уникальными физиологическими характеристиками. Помимо этого, результаты диссертации используются в учебном процессе на кафедре высшей математики Таганрогского технологического института Южного федерального университета в курсах «Математические методы искусственного интеллекта», «Современные проблемы прикладной математики», «Практикум решения задач на ЭВМ». Использование результатов работы подтверждено соответствующими актами.
Апробация работы. Материалы исследования докладывались и получили положительную оценку на II Международной научной конференции «Интеллектуальные системы принятия решений и прикладные аспекты информационных технологий» (г. Евпатория, 2006); Восьмом научно-практическом семинаре «Практика и перспективы развития партнерства в сфере высшей школы» (Донецк, 2007); III Международной научной конференции «Интеллектуальные системы принятия решений и прикладные аспекты информационных технологий» (г. Евпатория, 2007); Второй Международной конференции «Системный анализ и информационные технологии» (Обнинск, 2007), а также на рабочих семинарах и профессорско-преподавательских конференциях ТТИ ЮФУ.
Публикации. По результатам исследований, проведённых в рамках темы диссертационной работы, опубликовано 17 печатных работ, из них три работы в изданиях, входящих в «Перечень ведущих научных журналов и изданий, выпускаемых в Российской Федерации», утвержденных ВАК.
Структура и объем работы. Диссертационная работа состоит из введения, 4 глав, заключения, библиографического списка, включающего 83 наименования, и приложений на 38 стр. Основной текст работы изложен на 139 листах машинописного текста, содержит 44 рисунка, 5 таблиц.
СОДЕРЖАНИЕ РАБОТЫ
Во введении обосновывается актуальность темы диссертации, а также формулируются цели исследования и приводятся основные результаты работы и их научная новизна.
В первой главе введено определение основного понятия текстурного анализа, а именно текстуры, оно базируется на трех составляющих: текстурный элемент, правило смещения, текстурные функционалы. Впервые определение текстуры было введено Coggins, но оно не было строго формализовано. Затем попытки введения определения были предприняты Tamura, Sklansky, Haralick, но, как и в предыдущих случаях, определение вводилось на интуитивном уровне без строгих правил. Далее определение текстуры ввел Четвериков, но он не определил понятие текстурного изображения, а также способа выбора размера элементарной части текстуры и правила смещения элемента.
В данной диссертационной работе рассматриваются только периодические текстуры.
Определение 1. Идеальной текстурой называется такое непрерывное изображение 
, которое представляет собой периодическую функцию 
, где 
, 
периоды функции по оси 
и 
соответственно.
Определение 2. Участок идеальной текстуры 
, рассматриваемый в области 
, размеры которой изменяются в пределах, определяемых значениям периодов 
, 
функции текстуры, будем называть текстурным элементом и обозначать 
.
Определение 3. Текстурной характеристикой (функционалом) является скалярная величина, которая получается в результате действия отображения 
, 
, 
, 
– область текстуры.
Правило смещение текстурного элемента определяется следующим: 
, где 
– позиции пикселей текстурного элемента до смещения, 
– позиции текстурного элемента после его смещения по указанному правилу, 
– угол поворота элемента, 
– коэффициент растяжения/сжатия, 
– параллельный перенос относительно оси 
соответственно. Показано, что смещение элемента образует группу по операции умножения.
Предложен алгоритм определения оптимального размера текстурного элемента для случая аддитивной текстурной характеристики. Решение данной задачи позволит выделить текстурный элемент из целого изображения и найти такие значения характеристик, которые необходимы для точной идентификации всей текстуры. Зафиксируем некоторую прямоугольную подобласть 
области текстуры, верхний левый угол которой совпадает с верхним левым углом изображения, и рассмотрим всевозможные подобные области для нее. Эти подобласти образуют некоторый класс 
. Рассмотрим значения текстурных характеристик, рассчитанные в каждой области из одного класса. Все эти значения образуют некоторую функцию 
. Проанализировав значения функции 
при различном выборе подобластей из одного класса, легко заметить, что значения текстурной характеристики периодически повторяется с поправкой на некоторое число. Ситуация повторяется при выборе другого класса подобия областей. В работе доказана теорема.
Теорема 1. Если функция 
строится на основе аддитивной текстурной характеристики и выполняется следующее равенство
(1),
, 
, 
, 
, 
минимальна по площади среди возможных областей из 
, то найдется единственный класс подобия, в котором выполняется (1) и 
является областью текстурного элемента.
В главе показано соответствие введенного определения текстуры известным методам текстурного анализа.
Во второй главе исследуется статистический метод текстурной сегментации, основанный на матрице взаимного расположения градаций тона. Статистические методы вычисления текстурных характеристик основаны на одной общей идеи. При формировании функционала пиксели изображения группируются по значениям интенсивности, как в методах первого порядка, либо по взаимному расположению, как в методах второго порядка. При этом вычисление характеристик основано на построении некоторых промежуточных массивов. Этот факт приводит к выводу, что существует некоторая общая закономерность формирования этих промежуточных массивов и текстурных характеристик. В работе предлагается использовать интеграл Лебега как естественный математический аппарат для обобщения всех этих методов. Если интеграл Лебега 
брать от функции изображения 
по области 
, которая содержит в себе точки с определенными значениями интенсивности или перепадов интенсивностей, то будет происходить группировка по этим значениям и в результате при помощи данного интеграла можно рассчитать текстурные характеристики для методов первого порядка. С целью формирования текстурных функционалов для методов второго порядка необходимо учесть взаимное влияние пикселей. Для этого в простейшем случае рассмотрим производную от функции изображения и возьмем интеграл Лебега 
, 
, 
от нее. При расчете интеграла происходит группировка по значению перепадов интенсивности. На основе вычисленного интеграла легко выразить элементы известной гистограммы перепадов интенсивности. Далее рассмотрим разложение функции в ряд Тейлора и продолжим процедуру вычисления интеграла Лебега: 
, 
, 
. В результате можно получить элементы двумерной гистограммы распределения, в которой учитывается не только значение интенсивности пикселя, но и значения перепада интенсивности в направлении, определяемом некоторым вектором смещения. Учитывая большее количество членов разложения, можно получить гистограммы более высокого порядка, которые учитывают более «тонкие» зависимости пикселей. Тем самым дан новый способ построения иерархии вспомогательных массивов для расчета текстурных характеристик статистических методов.
Исследуем структуры парной взаимосвязи пикселей текстурного изображения, обусловленной некоторым вектором смещения 
. Для этого введем в рассмотрение граф 
. Вершины его соответствуют позициям пикселей. Множество ориентированных ребер образовано путем соединения каждой вершины с другой, находящей на расстоянии и в направлении, определяемом вектором 
. Далее введем в рассмотрении граф 
, вершины которого соответствуют значениям интенсивности, присутствующим на изображении. Каждое ориентированное ребро соответствует наличию пары пикселей, связанных вектором 
. Построенный граф 
представляет собой структуру перепадов тонов на изображении текстуры. Построим матрицу 
смежности для 
. Таким образом, каждый элемент 
матрицы 
будет представлять собой количество упорядоченных пар пикселей с интенсивностями 
и 
, находящихся друг от друга на расстоянии, в направлении, определяемом вектором 
. Элементы матрицы смежности графа взаимосвязи обладают обширной информацией о текстурном изображении. Матрица 
в точности соответствует известной матрице взаимного расположения градаций тона 
.
Определение 4. Матрицей взаимного расположения градаций тона называют матрицу вида 
, где 
- вектор смещения,
, 
– координаты пикселей в 
.
В главе 2 построены инвариантные матрицы 
относительно углов поворота изображения кратных 
. Получение подобных инвариантов необходимо для проведения качественной сегментации. Матрица 
, инвариантная относительно углов поворота изображения кратных 
, получена в результате усреднения по двум противоположным направлениям для вектора смещения 
: 
. Для построения матрицы 
инвариантной относительно углов поворота изображения кратных 
необходимо выполнить усреднение по четырем направлениям: 
. Количество операций, необходимых для расчета матрицы 
составляет 
, где 
- размеры подобласти, по которой происходит расчет матрицы, для матрицы 
- 
, для матрицы 
- 
.
В данной главе решена задача кластеризации множества функционалов по этому принципу схожести «статистического поведения». С этой целью проведен корреляционный анализ указанных функционалов, который позволил выявить наличие линейной статистической зависимости между ними и избавиться от излишней информативности количества текстурных характеристик, затем кластеризация на основе транзитивного замыкания. В результате было показано, что только следующие текстурные характеристики обладают линейной независимостью: корреляция 
, однородность 
, энтропия 
, автокорреляция 
, тень кластера 
, выпуклость кластера 
.
Текстурная сегментация является одной из сложных задач анализа текстур по причине отсутствия априорной информации о количестве текстур, присутствующих на изображении. В главе предлагается метод определения количества текстур, основанный на следующей идее. По всему исходному изображению методом «скользящего окна» рассчитываются текстурные характеристики. Далее, по известным значениям функционалов строится гистограмма их распределения. Каждая текстура, присутствующая на изображении обладает определенным значением текстурной характеристики, поэтому количество максимумов соответствует количеству текстур на исходном изображении.
В третьей главе исследуются марковские случайные поля (МСП), как способ моделирования текстур. В работах Cross МСП использовались для синтеза текстур, Chellappa и Khotanzad на основе МСП решали задачи классификации текстур, а Cohen и Therrien – сегментации.
Определение 5. Пусть 
некоторое конечное множество позиций или множество узлов; для каждого узла 
через 
обозначим некоторое конечное пространство состояний 
. Декартово произведение 
назовем пространством конечных конфигураций 
.
Определение 6. Семейство 
подмножеств 
будем называть системой окрестностей если 
и 
тогда и только тогда, когда 
.
Определение 7. Подмножество 
из 
будем называть кликой, если любые два различных элемента из 
являются соседями (принадлежат одной окрестности).
Определение 8. 
называется МСП на сетке 
по отношению к системе окрестностей 
тогда и только тогда, когда выполняются следующие условия:
1) 
, 
;
2) 
.
Выше дано определение МСП в терминах локальных характеристик. Глобальной характеристикой МСП является распределение Гиббса (2) с некоторой энергетической функцией (3), рассчитанной по кликам:
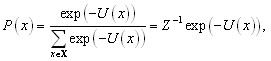(2)
(3)
Оба подхода эквиваленты в соответствии с теоремой Хаммерсли-Клиффорда.
В зависимости от вида энергетической функции существует множество моделей МСП. Наиболее точно описывающей текстуры является авторегрессионная модель, которая представляет собой: 
, где 
- белый шум с дисперсией 
. Именно эта модель выбрана для дальнейших исследований. Преобразовав к изображению с нулевым математическим ожиданием, получаем: 
. Для корректной оценки коэффициентов взаимосвязи пикселей все множество пикселей разбивается на внутреннее 
и внешнее 
. Каждая точка множества 
принадлежит ему вместе со своей окрестностью. Для оценки коэффициентов взаимосвязи необходимо решить СЛАУ 
. Вектор свободных членов 
представляет собой точки внутреннего множества. Строки матрицы 
– соседи каждой точки множества 
. Предлагается использовать псевдообращение матрицы коэффициентов системы методом Гревилля 
. Метод позволяет избежать вычисления детерминантов и является вычислительно устойчивым. Оценки являются наилучшим приближением в смысле метода наименьших квадратов для решения данного СЛАУ. Все оценки значимы.
Важным параметром МСП является порядок модели (количество пикселей, входящих в неё). Для её решения воспользуемся методами корреляционного анализа. Разобьем все изображение на непересекающиеся участки. В каждом участке рассчитаем корреляционную матрицу для значения интенсивностей пикселей некоторой окрестности заведомо высокого порядка. Затем вычислим среднюю корреляционную матрицу для всего изображения и проанализируем значения коэффициентов корреляции центрального пикселя и пикселей смежных с ним. В табл. 1 представлены результаты анализа. Первый столбец соответствует коэффициенту корреляции, второй – определяет значимость на уровне 
(значимый коэффициент корреляции помечен 1, незначимый 0) коэффициента, третий – порядок окрестности.
Для моделирования текстур окрестность не должна быть слишком маленькой, так как не будут учтены все взаимосвязи, но и не должна быть слишком большой, так как в модель будут включены пиксели слабо связанные друг с другом. Анализ показывает, что для построения модели МСП целесообразно брать окрестности порядка 4-5.
В результате исследований обнаружено, что тесная зависимость наблюдается только у пикселей порядка 1-2, поэтому логично предположить, что линейная модель взаимосвязи не является наиболее точно моделирующей зависимость пикселей.
Таблица 1
Коэффициенты корреляции
| коэфф. корр. | значи-мость. | поря-док | коэфф. корр | значи- мость | поря- док | коэфф. корр | значи-мость. | поря- док | ||
| 0.72 | 1 | 1 | 0.34 | 1 | 4 | 0.09 | 0 | 7 | ||
| 0.72 | 1 | 1 | 0.33 | 1 | 4 | 0.09 | 0 | 7 | ||
| 0.72 | 1 | 1 | 0.35 | 1 | 4 | 0.08 | 0 | 7 | ||
| 0.72 | 1 | 1 | 0.35 | 1 | 4 | 0.08 | 0 | 7 | ||
| 0.63 | 1 | 2 | 0.15 | 0 | 5 | 0.07 | 0 | 8 | ||
| 0.62 | 1 | 2 | 0.15 | 0 | 5 | 0.06 | 0 | 8 | ||
| 0.59 | 1 | 2 | 0.14 | 0 | 5 | 0.07 | 0 | 8 | ||
| 0.64 | 1 | 2 | 0.14 | 0 | 5 | 0.06 | 0 | 8 | ||
| 0.43 | 1 | 3 | 0.14 | 0 | 6 | |||||
| 0.42 | 1 | 3 | 0.13 | 0 | 6 | |||||
| 0.43 | 1 | 3 | 0.13 | 0 | 6 | |||||
| 0.43 | 1 | 3 | 0.12 | 0 | 6 | |||||
| 0.33 | 1 | 4 | 0.08 | 0 | 7 | |||||
| 0.33 | 1 | 4 | 0.08 | 0 | 7 | |||||
| 0.34 | 1 | 4 | 0.09 | 0 | 7 | |||||
| 0.34 | 1 | 4 | 0.08 | 0 | 7 |
В главе исследованы различные модели взаимосвязи. Далее приведены результаты регрессионного анализа для некоторого тестового изображения. Линейная модель: 
, оценка дисперсии ошибок = 0.12, коэффициент детерминации = 0.79; логарифмическая модель: 
, оценка дисперсии ошибок = 105.25, коэффициент детерминации = 0.52; гиперболическая модель: 
, оценка дисперсии ошибок = 230.23, коэффициент детерминации = 0.37; показательная модель: 
, оценка дисперсии ошибок = 0.07, коэффициент детерминации = 0.89; степенная модель: 
, оценка дисперсии ошибок = 0.02, коэффициент детерминации = 0.95.
Анализ для различных тестовых изображений показал, что наиболее точными моделями являются показательная и степенная. Факт высокой аппроксимации легко объясним, так как степенная модель является базисом, а показательная – представляющей системой, результаты подтверждены экспериментально.
Для реализации сегментации исходное изображение рассматривается как состоящее из двух изображений 
: поле яркости 
(исходное изображение) и поле меток 
(результат сегментации). Вводятся априорные модели для поля яркости (4) с энергетической функцией (5) и поля меток (6) с энергетической функцией (7).
(4)
(5)
(6)
, 
(7)
Задача сегментации может быть сформулирована, как процесс оптимизации, включающий в себя максимизацию апостериорной информации:
.
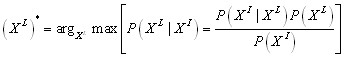Поиск всевозможных конфигураций изображения меток 
для глобального оптимума слишком громоздок в плане вычислений. Поэтому для решения данной задачи предлагается итерационный метод детерминистической релаксации для поиска локального оптимума. Изображение интенсивностей рассматривается как изображение, составленное из множества подизображений 
размером 
, центр каждого из которых находится в каждом пикселе 
. 
называют энергетическим окном. В каждом таком окне текстурные метки предполагаются однородными, т.е. все пиксели в этом окне принадлежат одной текстуре.
Моделирование текстур, хотя обладает преимуществом качества описания закономерностей изменения градаций тона, является вычислительно затратной процедурой. Для анализа реальных изображений в практических приложениях необходимы высокие скорости обработки. В работе изображение предлагается рассматривать как набор одномерных независимых случайных процессов, в отличие от предыдущего двумерного случая МСП. Для того, чтобы провести текстурную сегментацию, необходимо найти точки переключения с одной текстуры на другую, т.е. определить переход от одного участка стационарности к другому. На рис. 1 б) представлена строка изображения с рис. 1 а).
Визуально анализируя график, легко заметить, что наблюдается 3 участка стационарности. Если на всех рассчитать математическое ожидание, то каждый соседний участок будет обладать своим значением математического ожидания. Для решения задачи определения стационарных участков в работе предлагается использовать метод, разработанный Броневичем А.Г. и Каркищенко А.Н. Делается предположение о минимальной длительности стационарного участка и вводится дискриминантная функция, в данном случае она вводится на основе математического момента первого порядка: 
где 
- точка на середине стационарного участка 
, 
, 
, 
- длительность стационарного участка. Чем больше значения функции 
, тем выше вероятность появления точки перехода.
 |  |
| а) | б) |
Рис. 1. Изображение текстуры и ее строчная развертка
Значение функции 
рассчитываются для всех точек изображения. Затем вводится пороговое значение, на основе которого выявляются нестационарные точки, образующее множество 
. Далее все множество нестационарных точек 
необходимо кластеризовать по нестационарным участкам. С целью сглаживания вводится транзитивное замыкание функции 
, а именно, функция 
, 
. Тогда критерий принадлежности двух нестационарных точек одному нестационарному участку выглядит следующим образом. Будем считать, что точки 
при 
, 
, 
, принадлежат одному нестационарному участку в том и только том случае, если 
, 
. Функции 
и 
для строки изображения с рис 1 представлены на рис. 2.
Рис. 2. Дискриминантная функция, её транзитивное замыкание и порог
Для определения точки перехода в одном нестационарном участке можно воспользоваться формулой: 
. При сегментации изображения отдельно обрабатывается каждая строка и каждый столбец изображения. В результате текстурные границы получаются незамкнутыми, с целью их замыкания используется волновой алгоритм Ли, тем самым достигается определение текстурных границ.
В четвертой главе приведены общие сведения об изображениях полученных в радиочастотном диапазоне, экспериментальные исследования методов, детально изложены алгоритмы текстурной сегментации для всех исследуемых методов, а также производится оценка сложности статистических методов текстурной сегментации, сравнение качества работы разработанных методов. Для каждого метода приведены примеры работы алгоритмов сегментации на изображениях полученных в радиочастотном диапазоне.
Процесс сегментации для метода на основе матрицы взаимного расположения состоит в следующем.
1. Сканирование «окном» изображения и расчет в каждой его позиции указанной матрицы и текстурных характеристик.
2. Кластеризация при помощи метода K-means.
Оценка сверху количества операций, необходимых для сегментации изображения методом, основанным на построении матрицы взаимного расположения градаций тона, составляет 
операций, где 
и 
- размеры изображения, 
- размеры сканирующего окна, 
- количество градаций тона, 
- размерность вектора характеристик, 
- количество итераций для реализации метода 
-means, 
- количество текстур. Предложенная во второй главе матрица инвариантная относительно углов поворота изображений позволяет улучшить качество сегментации, ошибка первого рода снижена в среднем на 3%, второго – на 4%.
Алгоритм сегментации на основе МСП состоит в следующем.
1. Преобразуем изображение интенсивностей в изображение с нулевым математическим ожиданием.
2. Разбиваем изображение на непересекающиеся области и рассчитываем параметры моделей в каждой из них.
3. Разбиваем все области на число кластеров, равных числу текстур.
4. Оцениваем параметры модели для каждого кластера.
5. Детерминистическая релаксация: рассчитываем суммарную энергию Гиббса по полю интенсивностей и меток внутри энергетического окна. Обновление изображения меток происходит тем классом, который обладает наименьшей энергией Гиббса. Процесс продолжается до тех пор, пока общая энергия не перестанет меняться.
Количество операций, необходимое для реализации сегментации данным методом: 
, где 
- размеры изображения, 
- размеры сканирующего окна, 
- размер модели, 
- количество итераций для реализации предварительной кластеризации, 
- количество текстур, 
- количество итераций детерминистической релаксации. Предложенный в работе метод выбора уравнения взаимосвязи пикселей позволяет повысить качество сегментации, ошибка первого рода снижена в среднем на 4%, второго – на 6%. Процесс сегментации для метода на основе выделения стационарных участков случайных последовательностей можно представить следующим образом.
1. Построчное горизонтальное сканирование изображения и выделение нестационарных участков на основе дискриминантной функции.
2. На каждом нестационарном участке определение местоположения точки переключения случайного процесса после горизонтального сканирования изображения.
3. Постолбцовое вертикальное сканирование изображения и выделение нестационарных участков на основе дискриминантной функции.
4. На каждом нестационарном участке определение местоположения точки переключения случайного процесса после вертикального сканирования изображения.
5. Замыкание полученных граничных точек (совокупности всех точек переключения случайного процесса).
Результаты сегментации представлены на рис. 3. Исходное изображение представлено на рис. 3 а), на рис. 3 б) результат сегментации для метода на основе матрицы взаимного расположения градаций тона, на рис. 3 в) результат для метода на основе МСП, на рис. 3 г) для метода, основанного на выделении стационарных участков случайных последовательностей.
 |  |
| а) | б) |
 |  |
| д) | г) |
Рис. 3. Результаты сегментации статистических методов
Для реализации метода сегментации необходимо 
операций, где 
- размеры изображения, 
- минимальная длительность стационарного участка. Оценка является оценкой сверху. Ошибка первого рода сегментации для данного метода на тестовых изображениях составляет в среднем 5%, второго – 4%.
В приложении приводится листинг программного комплекса, реализующего текстурную сегментацию, набор тестовых изображений из альбома Бродаца и таблица результатов тестирования в сравнении с известными методами.
ОСНОВНЫЕ РЕЗУЛЬТАТЫ
При решении поставленных в диссертационной работе задач получены следующие новые теоретические и прикладные результаты.
1. Предложено определение текстуры, содержащее в себе три составляющих: текстурный элемент, правило его смещения и текстурные функционалы. Разработан метод определения размера текстурного элемента.
2. Построен обобщенный подход к статистическим методам первого и второго порядка на основе вычисления интеграла Лебега от разложения функции изображения в ряд Тейлора. Для матрицы взаимного расположения градаций тона предложен способ построения её инвариантов относительно наиболее распространенных углов поворотов изображения.
3. Предложен метод статистического анализа текстурных характеристик на основе корреляционного анализа и кластеризации при помощи транзитивного замыкания с целью устранения имеющейся избыточности функционалов.
4. Разработаны методы оценки параметров изображения, включающие определение количества текстур и оценку порядка модели МСП, синтезирован алгоритм выбора уравнения взаимосвязи пикселей окрестности, основанный на регрессионном анализе, в совокупности позволяющие проводить автоматизированную сегментацию с высокой степенью достоверности.
5. Предложен метод текстурной сегментации на основе поиска точек переключения случайных процессов для двумерных изображений.
6. Разработан программный комплекс, реализующий текстурную сегментацию.
Основные публикации по теме диссертации
1. Патана Е.И. Анализ текстурных характеристик, используемых для сегментации изображений // Сборник трудов VIII Всероссийской научной конференции студентов и аспирантов «Техническая кибернетика, радиоэлектроника и системы управления». Таганрог: ТТИ ЮФУ, 2006. – С. 224.
2. Патана Е.И. Текстурная сегментация изображений с помощью построения матрицы взаимного расположения градаций тона. // Сборник трудов II Международной научной конференции «Интеллектуальные системы принятия решений и прикладные аспекты информационных технологий». Евпатория: ХМИ, 2006. – С. 185-188.
3. Патана Е.И. Построение инвариантных текстурных характеристик относительно углов поворота изображений // Сборник трудов Восьмого Международного научно-практического семинара «Практика и перспективы развития партнерства в сфере высшей школы». Донецк: Известия ДонНТУ-ТТИ ЮФУ, №7, 2007. – С. 226-232.
4. Патана Е.И. Метод расчета количества текстур для выполнения сегментации изображений // Сборник трудов IV-й Международной конференции «Интегрированные модели и мягкие вычисления в искусственном интеллекте». Коломна 28-30 мая 2007 – С. 220-224.
5. Патана Е.И. Корреляционный анализ текстурных характеристик // Сборник трудов Второй Международной конференции «Системный анализ и информационные технологии САИТ-2007», Обнинск, Россия 10-14 сентября 2007 – С. 221-225.
6. Патана Е.И. Использование псевдообращения в задаче оценки параметров гауссовской модели Марковских случайных полей // Сборник трудов IV Международной научной конференции «Интеллектуальные системы принятия решений и прикладные аспекты информационных технологий». Евпатория: ХМИ, 2008. – С. 126-129.
7. Патана Е.И. Текстурная сегментация изображений на основе их моделирования // Сборники трудов Восьмого и Девятого Международного научно-практического семинара «Практика и перспективы развития партнерства в сфере высшей школы». Донецк: Известия ДонНТУ-ТТИ ЮФУ, №8, 2008 – С. 141-145.
8. Патана Е.И. Алгоритм сегментации и оценки параметров изображения, как реализации Марковского случайного поля // Материалы III Всероссийской конференции с международным участием «Математика, ее приложения и математическое образование», Улан-Удэ: ВСГТУ, 23-28 июня, 2008. – С. 252-255.
9. Патана Е.И. Статистический анализ и кластеризация основных текстурных функционалов // Известия ЮФУ. Технические науки. № 4. Тематический выпуск "Интеллектуальные САПР". - Таганрог: ТТИ ЮФУ, 2008. – С. 192-198.
10. Патана Е.И. Методы определения априорных параметров для текстурной сегментации изображений на основе марковских случайных полей. // Научно-технические ведомости СПбГПУ. «Информатика. Телекоммуникации. Управление», Санкт-Петербург: СПбГПУ, 2009. – С. 53-61.
11. Патана Е.И. Метод определения размера модели Марковского случайного поля. // Известия ЮФУ. Технические науки. №8. Тематический выпуск "Актуальные проблемы математического моделирования". - Таганрог: ТТИ ЮФУ, 2009. – С. 206-212.
Все перечисленные работы написаны без соавторов, результаты, опубликованные в них, принадлежат автору.
______________________________________________________________________________
Типография ТТИ ЮФУ, ГСП 17А, Таганрог, ул. Энгельса, 1. Заказ № Тираж 100 экз.
