Разработка и исследование схем детерминированного поиска на основе сортировки с приложением к идентификации оцифрованных объектов различных типов
На правах рукописи
Белоконова Светлана Сергеевна
РАЗРАБОТКА И ИССЛЕДОВАНИЕ СХЕМ ДЕТЕРМИНИРОВАННОГО ПОИСКА НА ОСНОВЕ СОРТИРОВКИ С ПРИЛОЖЕНИЕМ
К ИДЕНТИФИКАЦИИ ОЦИФРОВАННЫХ ОБЪЕКТОВ
РАЗЛИЧНЫХ ТИПОВ
Специальность:
05.13.17 – Теоретические основы информатики
А В Т О Р Е Ф Е Р А Т
диссертации на соискание ученой степени
кандидата технических наук
Таганрог 2007
Работа выполнена в ГОУВПО «Таганрогский государственный педагогический институт».
Научный руководитель: доктор технических наук,
профессор Ромм Яков Евсеевич
Официальные оппоненты: доктор технических наук,
профессор Финаев Валерий Иванович
кандидат технических наук,
старший научный сотрудник Сапрыкин Владимир Абрамович
Ведущая организация: Ростовский государственный университет
путей сообщения (РГУПС)
Защита состоится « 24 » мая 2007 г. в 14.20 на заседании диссертационного совета Д 212.208.21 при федеральном государственном образовательном учреждении высшего профессионального образования «Южный федеральный университет» по адресу: 347928, г. Таганрог, пер. Некрасовский, 44, ауд. Д-406.
С диссертацией можно ознакомиться в библиотеке Технологического института федерального государственного образовательного учреждения высшего профессионального образования «Южный федеральный университет» в г. Таганроге.
Автореферат разослан « 20 » апреля 2007 г.
| Ученый секретарь диссертационного совета Д 212.208.21 доктор технических наук, профессор |  | Бабенко Л.К. |
ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ
Проблема поиска, сбора и обработки информации принадлежит к числу основных задач информатики. Ее актуальность возрастает с ростом объема информации в электронном виде, с ростом ресурсов, доступных в сети Internet. Особую актуальность приобрели вопросы, связанные с поиском и распознаванием оцифрованной информации различного формата и типа данных, включая текстовую, графическую, аудио- и видеоинформацию. Существующие методы и подходы не вполне обеспечивают точность, релевантность результатов поиска запросу, не совмещают в требуемой мере поиск с распознаванием. В частности, это относится к поиску данных различных несовместимых типов, к обработке плохо структурированной информации. Поэтому актуальна разработка новых методов, позволяющих повысить эффективность, расширить область применения схем поиска, включая полнотекстовый поиск при организации электронных библиотек и каталогов, где проблема определяется растущим количеством пользователей, не обладающих профессиональными навыками при поиске информации на языке запросов. Наиболее масштабные исследования в области информационного поиска относятся к 90-м годам прошлого века, они интенсивно продолжаются в настоящее время. При этом характерно, что большинство предлагаемых методов эффективны на больших объемах данных, которые не могут быть подвергнуты анализу по выделению структуры. Одним из направлений исследования является применение известных методов распознавания к поиску оцифрованной информации различного типа. Методы адаптивного распознавания образов и семантические сети, опирающиеся на теорию нейронных сетей, осуществляют поиск текстовой, графической, аудио и видео, а также числовой информации. В диссертационной работе наряду с данными вопросами рассматривается обратная задача – применение методов поиска к распознаванию. При этом предполагается не только расширение области поиска до объектов различных типов, но включается поиск и распознавание отдельных фрагментов объектов и их свойств, а также детерминированный поиск неисправностей. Актуальность последней задачи обусловлена тенденцией увеличения объема передаваемой информации, повышением функциональной и аппаратурной насыщенности сетей передачи данных, ростом требований на скорость и надежность передачи и, как следствие, на техническое, в частности, тестовое диагностирование сетей. В данном контексте актуальна задача разработки схем поиска и распознавания на единой основе.
Цель диссертационной работы заключается в разработке и исследовании единой алгоритмической схемы поиска на основе применения сортировки в качестве конструктивного алгоритма. Более точно, исследуется использование подстановок индексов, формируемых сортировками, с целью применения к поиску данных различных типов. На основе исследования конструируются схемы с условиями поиска семантического характера, разрабатываются видоизменения схем поиска для распознавания и идентификации. Конструируемые схемы должны включать как схемы текстового поиска, поиска файлов, так и схемы поиска данных вещественного типа, а также должны осуществлять идентификацию объектов одновременно по нескольким разнотипным признакам, при этом отличаясь единством конструкции, устойчивостью и параллелизмом.
Для достижения цели в диссертационной работе поставлены следующие задачи:
- Сконструировать распараллеливаемый метод применения сортировки для поиска на ее основе локально минимальных и локально максимальных значений элементов числовой последовательности. Применить метод для детерминированного поиска символов, слов и словосочетаний в тексте, для обнаружения скрытых закономерностей плохо структурированного текста.
- На основе взаимно однозначного соответствия индексов в форме подстановки, определяемой сортировкой, сконструировать схемы с использованием обработки числовых выражений для поиска данных строкового и вещественного типа, сконструировать поиск в тексте как алгоритм поиска нулей и экстремумов числовой последовательности, сопоставленной тексту.
- Сконструировать схему, позволяющую выполнить поиск по математическим условиям чисел и векторов как минимумов нормы разности между искомым элементом многомерного пространства и эталонным элементом из этого пространства.
- Сконструировать метод индексной идентификации текстовых фрагментов по условиям в виде сложных математических выражений и выражений, включающих особенности семантического характера, совместить поиск с распознаванием текстовых особенностей.
- Синтезировать схему детерминированного поиска одновременно по нескольким маскам с учетом взаимного расположения полных и частичных комбинаций масок, расстояний между ними и изменяемости словоформ.
- Разработать видоизменение схемы поиска для случая поиска текстовых файлов, содержащих совокупность масок с заданными условиями относительно их взаимного расположения.
- Разработать видоизменение схемы поиска для случая поиска объектов (и их свойств) различных типов, включая поиск группы разнотипных файлов, адаптировать схему для идентификации объектов общего вида на основе формализации признаков.
- Разработать видоизменение базовой схемы поиска для распознавания и идентификации плоских растровых изображений.
- На той же основе синтезировать распараллеливаемый алгоритм идентификации неисправностей цифровых устройств.
- Выполнить сравнительный анализ схем с известными методами поиска, включая оценки временной сложности с проведением программных экспериментов.
Методы исследования опираются на теоретические основы информатики, методы распознавания образов, современные информационные технологии, методы параллельных сортировок и поиска.
Достоверность результатов обосновывается математическими доказательствами, оценками временной сложности, результатами программного моделирования и эксперимента.
Научная новизна диссертационной работы вытекает из применения сортировки в качестве конструктивной основы поиска, при этом поиск строится как алгоритм идентификации нулей и экстремумов числовой последовательности, сопоставленной объектам произвольного типа, включая растровые изображения и неисправности электронных устройств. На основе идентификации всех локальных и глобальных экстремумов, а также идентификации структуры окрестности каждого экстремума числовой последовательности, сопоставленной множеству исследуемых объектов, формируется вектор признаков, включающий все отличительные экстремальные особенности искомых объектов и их свойств. Отличие подхода от известных методов в том, что предложенные схемы, достигая результатов обычного поиска по вхождению подстрок в строки, включают поиск данных вещественного типа с заданной границей погрешности, позволяют выполнить поиск векторов как минимумов нормы разности между искомым элементом многомерного пространства и эталонным вектором в этом пространстве, включают поиск данных различных типов, распространяются на идентификацию объектов и их свойств, включая неисправности цифровых устройств.
Конкретно, научная новизна характеризуется следующим образом:
- Сконструирован распараллеливаемый метод применения сортировки для поиска на ее основе локально экстремальных элементов числовой последовательности. С использованием кодовой таблицы символов метод применяется для детерминированного поиска в тексте элементов строкового типа. Метод отличается от известных применением сортировки в качестве конструктивной базовой части схемы поиска, использованием индексов сортируемых элементов в качестве адресных идентификаторов искомых элементов, включением в единую схему поиска элементов строкового и числового (вещественного) типа.
- Предложена схема на основе сортировки с использованием обработки числовых выражений для поиска данных строкового и вещественного типа, которая отличается от известных по построению в форме алгоритма поиска нулей и экстремумов числовой последовательности, сопоставленной тексту, а также тем, что распространяет поиск на числовые данные с плавающей точкой при заданной границе погрешности. Схема распространяется на последовательность точек многомерного нормированного пространства, где осуществляется поиск минимумов нормы разности между текущим элементом последовательности и эталонным элементом пространства.
- Разработан метод индексной идентификации множества произвольных текстовых фрагментов по условиям, включающим семантические особенности, и отличающийся совмещением поиска с распознаванием заданных особенностей искомых объектов.
- Предложена схема детерминированного поиска одновременно по нескольким маскам с учетом их взаимного расположения и изменяемости словоформ. Схема отличается построением поиска по экстремальным особенностям сопоставленных тексту числовых последовательностей, а также качеством идентификации составных объектов в произвольном взаимном расположении элементов.
- Предложена схема поиска текстовых файлов по совокупности масок с заданным взаимным расположением, которая отличается от известных методов по построению без анализа вхождений подстроки в строку, детерминированными результатами поиска и параллелизмом.
- Сконструирована мультипликативная схема поиска по множеству масок с заданным взаимным расположением, для которой доказаны теоремы единственности и взаимно однозначного соответствия исследуемому тексту результатов поиска. Единственность идентификации по группам взаимно упорядоченных масок отличает схему от известных методов поиска.
- Предложена схема поиска конечного множества объектов различных типов, включая разнотипные файлы и объекты общего вида, на основе формализации признаков. Множественность типов искомых объектов отличает схему от известных методов поиска.
- Разработано преобразование основной схемы поиска для идентификации свойств объектов различного типа, включая идентификацию плоских оцифрованных изображений. Преобразованная схема, в частности, отличается применимостью к произвольному геометрическому месту точек на плоскости и обратимым преобразованием матрицы изображения
 в вектор размерности
в вектор размерности  .
. - Схема идентификации свойств объектов различного типа преобразована в распараллеливаемый алгоритм идентификации неисправностей цифровых устройств, который отличается применимостью к устройствам сравнительно общего вида.
- Выполнены программные эксперименты с предложенными схемами поиска и идентификации объектов на основе экстремальных закономерностей, извлекаемых с помощью сортировки из сопоставленных числовых последовательностей. Показан параллелизм предложенных схем, даны оценки временной сложности их максимально параллельной формы.
Основные положения, выносимые на защиту:
- Распараллеливаемый метод применения сортировки для поиска всех локально экстремальных и произвольно заданных элементов числовой последовательности с допустимой погрешностью, который распространяется на последовательности элементов многомерных нормированных пространств.
- Схема на основе сортировки с использованием обработки числовых выражений для поиска данных одновременно как строкового, так и вещественного типа, которая сводится к алгоритму поиска нулей и экстремумов числовой последовательности, сопоставленной тексту, обеспечивая поиск числовых данных с плавающей точкой при заданной границе погрешности.
- Мультипликативная схема текстового поиска по множеству масок с заданным взаимным расположением, для которой доказаны теоремы единственности и взаимно однозначного соответствия исследуемому тексту результатов поиска.
- Схема поиска конечного множества объектов различных типов, включая разнотипные файлы и объекты общего вида, на основе формализации признаков и извлечения скрытых экстремальных закономерностей данных с помощью сортировки.
- Преобразование основной схемы поиска для идентификации свойств объектов различного типа, включая идентификацию плоских оцифрованных изображений и поиск неисправностей. Преобразование, в частности, применимо к произвольному геометрическому месту точек на плоскости и осуществляет обратимое преобразование матрицы изображения
 в вектор размерности
в вектор размерности  .
.
Связь с плановыми исследованиями, проводимыми по месту выполнения диссертационной работы. Диссертационная работа выполнялась в рамках госбюджетной НИР «Математические методы устойчивой параллельной обработки, поиска и распознавания» (№ гос. регистрации 01.2.00106436, код ГРНТИ 28.23.15), проводимой на кафедре информатики ГОУВПО «ТГПИ» в рамках приоритетного направления развития науки и техники в РФ «Информационные и телекоммуникационные системы» в соответствии с перечнем критических технологий РФ «Технологии обработки, хранения, передачи и защиты информации» по направлению фундаментальных исследований «Информатика. Искусственный интеллект, системы распознавания образов, принятие решений при многих критериях».
Практическая ценность диссертационного исследования заключается в прикладном характере предложенных методов и алгоритмов. Разработанные схемы поиска могут быть составляющими редакторов языков программирования, операционных систем, их компьютерная реализация актуальна для систем автоматизации научных исследований, включая компьютерную обработку результатов физических экспериментов и компьютерное тестирование электронных устройств. Предложенные схемы применимы для упрощения и повышения эффективности навигации в существенных объемах информации на Web-серверах, при создании больших электронных архивов, включая электронные библиотеки. В целом, разработанные методы могут использоваться в системах электронного документооборота при росте массивов обрабатываемых полнотекстовых документов, могут применяться в качестве средств организации доступа к информации, включая те из них, которые примыкают к разряду систем искусственного интеллекта. В частности, представленные схемы могут играть роль при поиске документов по их содержанию в Internet для обеспечения адекватного выбора информации по запросу пользователя. Предложенные схемы идентификации разнотипных данных, включая изображения в формате BMP, могут использоваться для повышения эффективности поиска по содержанию.
Внедрение и использование результатов работы. Полученные в работе результаты использованы:
- В отделе автоматизации библиотеки Таганрогского государственного педагогического института при создании электронной библиотеки и информационного центра ГОУВПО «ТГПИ».
- В госбюджетной НИР «Математические методы устойчивой параллельной обработки, поиска и распознавания» (№ гос. регистрации 01.2.00106436, код ГРНТИ 28.23.15), проводимой на кафедре информатики ГОУВПО «ТГПИ».
- В учебном процессе кафедры информатики ГОУВПО «ТГПИ» в рамках курсов «Информатика», «Информационные системы», «Информационные технологии в математике», «Элементы абстрактной и компьютерной алгебры», «Использование информационных и коммуникационных технологий в образовании».
Апробация работы. Основные результаты работы докладывались на: I международной научно-практической конференции «Текст в системе высшего профессионального образования» (Таганрог, ТГПИ, 2003 г.); IX-XI международных конференциях «Математические модели физических процессов» (Таганрог, ТГПИ, 2003-2006 гг.); IV международной научно-практической конференции по программированию УкрПРОГ’ 2004 (Украина, Киев, 2004 г.); международной научно-практической конференции «Модернизация отечественного педагогического образования: проблемы, подходы, решения» (Таганрог, ТГПИ, 2005 г.); международной научной конференции «Оптимальные методы решения научных и практических задач» (Таганрог, ТРТУ, 2005 г.); семинарах «Теоретическая и прикладная информатика» кафедры информатики ТГПИ (Таганрог, 2001 – 2006гг.).
Публикации. По материалам диссертационной работы опубликовано 14 печатных работ общим объёмом 14,4 п. л., в том числе, 1 статья в журнале из списка допущенных ВАК РФ.
Структура и объём работы. Диссертационная работа состоит из введения, 3 глав основного раздела, списка литературы и 5 приложений. Основное содержание работы изложено на 156 страницах, включая список литературы из 149 наименований.
СОДЕРЖАНИЕ РАБОТЫ
Во введении обосновывается актуальность и характеризуется современное состояние проблем поиска и распознавания. На основе обзора основных методов и не решенных проблем ставятся цели и задачи исследования, формулируются основные положения, выносимые на защиту.
В первой главе конструируются алгоритмы применения сортировки и локализации на ее основе минимальных и максимальных значений числовой последовательности для поиска и распознавания символов, слов и словосочетаний в тексте. Рассматриваются применения данных алгоритмов для распознавания и идентификации сложных текстовых фрагментов.
В основе схемы лежит применение адресной устойчивой распараллеливаемой сортировки по ключу, сохраняющей на выходе входные индексы упорядоченных элементов (свойство обратной адресности), т.е. обладающей взаимно однозначным соответствием входных и выходных индексов. Одна из таких сортировок представляет собой разновидность сортировки подсчетом, для описания которой применяется матрица сравнений (МС). На пересечении ![]() -й строки и
-й строки и ![]() -го столбца МС находится результат сравнения элементов
-го столбца МС находится результат сравнения элементов ![]() и
и ![]() , отмечаемый знаком « + », если
, отмечаемый знаком « + », если ![]() , знаком « - », если
, знаком « - », если ![]() , и знаком « 0 », если
, и знаком « 0 », если ![]() . Число нулей и плюсов в
. Число нулей и плюсов в ![]() -м столбце над диагональю, включая диагональный элемент, складывается с числом минусов
-м столбце над диагональю, включая диагональный элемент, складывается с числом минусов ![]() -й строки справа от диагонали. Значение суммы
-й строки справа от диагонали. Значение суммы ![]() становится индексом
становится индексом ![]() -го элемента в отсортированном массиве:
-го элемента в отсортированном массиве: ![]() , с тем же индексом запоминается входной номер переставленного элемента:
, с тем же индексом запоминается входной номер переставленного элемента: ![]() .
.
Дополнительной составляющей конструируемой схемы поиска является оператор локализации экстремальных элементов. Локально минимальный элемент массива определяется как элемент меньший предшествующего и не больший последующего по отношению «<=». Оператор локализации минимумов последовательности из ![]() элементов имеет вид:
элементов имеет вид:
j:=1;while j<= n do begin FOR L:=1 TO j-1 do if abs(e[j]-e[j-L])<=eps then goto 22; Writeln (' ',c[e[j]],' ',e[j]);
22: j:=j+1; end;
Присоединение к процедуре сортировки оператора локализации минимумов влечет программную идентификацию всех локально минимальных элементов входного массива в окрестности радиуса ![]() . При
. При ![]() идентифицируются элементы, минимальные по отношению к соседним с ними. Значение
идентифицируются элементы, минимальные по отношению к соседним с ними. Значение ![]() именуется радиусом окрестности локализации минимума. Без повторной сортировки с незначительной модификацией оператора локализуются максимальные элементы. Экстремальные элементы можно найти и другими способами, однако изложенный обладает содержательной информацией, благодаря которой в дальнейшем идентифицируются не только экстремумы, но и вся внутренняя структура локализованной окрестности. При этом без повторения сортировки локализация и структура локальных экстремумов (что существенно для поиска) идентифицируются одновременно для всех требуемых значений
именуется радиусом окрестности локализации минимума. Без повторной сортировки с незначительной модификацией оператора локализуются максимальные элементы. Экстремальные элементы можно найти и другими способами, однако изложенный обладает содержательной информацией, благодаря которой в дальнейшем идентифицируются не только экстремумы, но и вся внутренняя структура локализованной окрестности. При этом без повторения сортировки локализация и структура локальных экстремумов (что существенно для поиска) идентифицируются одновременно для всех требуемых значений ![]() . На основании параллелизма сортировки экстремумы идентифицируются по максимально параллельной схеме.
. На основании параллелизма сортировки экстремумы идентифицируются по максимально параллельной схеме.
Схема поиска экстремальных элементов числовой последовательности по построению применима к целым и вещественным числам, а также к числам в формате с плавающей точкой типа двойной и повышенной точности. Использование этой числовой схемы по построению отличает конструируемый поиск от известных схем поиска по вхождению подстроки в строку.
В случае числового массива оператор локализации минимумов осуществляет поиск заданного числа как идентификацию нуля абсолютной величины разности между текущим элементом массива и заданным искомым числом. Пусть в числовой последовательности ![]() требуется найти заданное число
требуется найти заданное число ![]() . Последовательность
. Последовательность ![]() преобразуется к виду:
преобразуется к виду:
![]() (1)
(1)
и поступает на вход сортировки, после ее выполнения оператор локализации минимумов идентифицирует все нули, если они есть. По индексам ![]() идентифицированных нулей последовательности (1) можно обратится к элементам исходного массива: Writeln (a[e[j]],e[j]). Все такие элементы совпадут с числом
идентифицированных нулей последовательности (1) можно обратится к элементам исходного массива: Writeln (a[e[j]],e[j]). Все такие элементы совпадут с числом ![]() , если оно было элементом входной последовательности
, если оно было элементом входной последовательности ![]() . Описанный способ поиска применим к числам любого типа, его можно осуществлять с точностью до заданной границы погрешности. Схема выполняет поиск локально минимальных элементов числовой последовательности, отличающиеся от искомого не более чем на
. Описанный способ поиска применим к числам любого типа, его можно осуществлять с точностью до заданной границы погрешности. Схема выполняет поиск локально минимальных элементов числовой последовательности, отличающиеся от искомого не более чем на ![]() (идентификатор границы погрешности). Например, чтобы в последовательности
(идентификатор границы погрешности). Например, чтобы в последовательности  найти число
найти число ![]() с точностью до
с точностью до ![]() =
=![]() , на вход схемы подается последовательность, сформированная согласно (1):
, на вход схемы подается последовательность, сформированная согласно (1): ![]() 0.00000077709, 0.00000077709, 29.117, 0.00000077708, 5.244
0.00000077709, 0.00000077709, 29.117, 0.00000077708, 5.244![]() . Полученный массив сортируется, применяется оператор локализации минимумов, затем выполняется просмотр идентифицированных минимумов. Условие
. Полученный массив сортируется, применяется оператор локализации минимумов, затем выполняется просмотр идентифицированных минимумов. Условие ![]() выводит элементы, отличающиеся от искомого не более чем на
выводит элементы, отличающиеся от искомого не более чем на ![]() . При
. При ![]() будут найдены элементы 2,00600077709 с индексом 1 и 2,00600077708 с индексом 4. Изменение в операторе локализации минимумов заголовка цикла на
будут найдены элементы 2,00600077709 с индексом 1 и 2,00600077708 с индексом 4. Изменение в операторе локализации минимумов заголовка цикла на ![]() позволит выводить последовательно повторяющиеся (соседние) элементы, отличающиеся от искомого не более чем на
позволит выводить последовательно повторяющиеся (соседние) элементы, отличающиеся от искомого не более чем на ![]() . Способ применим для поиска чисел в заданном диапазоне с идентификацией максимума и минимума отклонения от искомого значения.
. Способ применим для поиска чисел в заданном диапазоне с идентификацией максимума и минимума отклонения от искомого значения.
Схема следующим образом переносится на поиск слов в массиве строковых элементов. Входному строковому массиву ![]() сопоставляется числовой массив из абсолютных величин разностей ASCII-кода символа, стоящего на заданной позиции слова входного массива, и ASCII-кода символа, указанного в маске поиска:
сопоставляется числовой массив из абсолютных величин разностей ASCII-кода символа, стоящего на заданной позиции слова входного массива, и ASCII-кода символа, указанного в маске поиска:
![]() (2)
(2)
В (2) ![]() – входной массив,
– входной массив, ![]() – номер позиции, заданной в маске,
– номер позиции, заданной в маске, ![]() – номер элемента массива
– номер элемента массива ![]() ,
,![]() – символ, заданный в маске,
– символ, заданный в маске, ![]() – элемент сопоставляемого числового массива
– элемент сопоставляемого числового массива ![]() . Поиск символов происходит как поиск локальных минимумов, которые в данном случае все оказываются нулями. Используя обратную адресацию, по индексам идентифицированных нулей можно обратиться к элементам входного массива строковых элементов, поскольку нумерация элементов обоих массивов сохраняется: если
. Поиск символов происходит как поиск локальных минимумов, которые в данном случае все оказываются нулями. Используя обратную адресацию, по индексам идентифицированных нулей можно обратиться к элементам входного массива строковых элементов, поскольку нумерация элементов обоих массивов сохраняется: если ![]() -й элемент массива
-й элемент массива ![]() удовлетворяет маске поиска, то
удовлетворяет маске поиска, то ![]() , отсюда искомые слова находятся по индексам нулевых элементов числового массива. Принципиально, что адресоваться к строковым элементам входного массива в рамках излагаемой схемы можно исключительно благодаря взаимно однозначному соответствию входных и выходных индексов сортируемых элементов, схема поиска существенно опирается на прямую и обратную адресность сортировки, которая используется не косвенно, а как основная конструктивная составляющая алгоритма поиска.
, отсюда искомые слова находятся по индексам нулевых элементов числового массива. Принципиально, что адресоваться к строковым элементам входного массива в рамках излагаемой схемы можно исключительно благодаря взаимно однозначному соответствию входных и выходных индексов сортируемых элементов, схема поиска существенно опирается на прямую и обратную адресность сортировки, которая используется не косвенно, а как основная конструктивная составляющая алгоритма поиска.
Схема поиска слов, содержащих заданный символ, переносится на поиск слов по комбинации нескольких символов. Для этого массиву слов сопоставляется числовой массив путем суммирования абсолютных величин разностей ASCII-кода символа входного массива и символа «маски» поиска с учетом соответствия позиций:
![]() (3)
(3)
где ![]() - числовое значение, сопоставленное
- числовое значение, сопоставленное ![]() -му слову,
-му слову, ![]() -
- ![]() -е слово,
-е слово, ![]() - номер позиции на которой расположена
- номер позиции на которой расположена ![]() -я маска поиска,
-я маска поиска, ![]() -
- ![]() -я маска поиска. Идентификация искомой комбинации символов основана на том, что сумма нулевых разностей сохранит нулевое значение. В сопоставленном числовом массиве выполняется поиск нулевого значения по описанной схеме. Искомые слова могли быть идентифицированы без применения оператора локализации минимумов, поскольку нули (если они есть) составляют первые элементы отсортированного массива, обратиться к соответствующим строковым элементам можно по сохраненным на выходе сортировки входным индексам (
-я маска поиска. Идентификация искомой комбинации символов основана на том, что сумма нулевых разностей сохранит нулевое значение. В сопоставленном числовом массиве выполняется поиск нулевого значения по описанной схеме. Искомые слова могли быть идентифицированы без применения оператора локализации минимумов, поскольку нули (если они есть) составляют первые элементы отсортированного массива, обратиться к соответствующим строковым элементам можно по сохраненным на выходе сортировки входным индексам (![]() ) этих нулей. Однако условие локализации может включать произвольно задаваемое значение радиуса локализации
) этих нулей. Однако условие локализации может включать произвольно задаваемое значение радиуса локализации ![]() , который можно использовать в качестве одного из условий поиска. В дальнейшем использование оператора локализации минимумов будет положено в основу определения меры сходства искомых элементов, затем этот оператор явится основой идентификации искомых элементов непосредственно по локальным и глобальным экстремумам сопоставленной числовой последовательности. Его описание в предварительно сконструированной схеме – существенная часть развиваемого в диссертации метода.
, который можно использовать в качестве одного из условий поиска. В дальнейшем использование оператора локализации минимумов будет положено в основу определения меры сходства искомых элементов, затем этот оператор явится основой идентификации искомых элементов непосредственно по локальным и глобальным экстремумам сопоставленной числовой последовательности. Его описание в предварительно сконструированной схеме – существенная часть развиваемого в диссертации метода.
Схема переносится на поиск текстовых фрагментов при более сложных признаках искомых фрагментов. В качестве признака может использоваться символ, сочетание символов, сочетание слов, предложений, значение радиуса ![]() , расстояние между символами, словами, предложениями. С помощью этих признаков можно организовать иерархию вложенных условий, применяя их заново к уже найденным фразам. Результат применения иерархически усложняющихся условий поиска – точная идентификация искомых фрагментов текста. При этом число вложений по построению схемы не ограничено. С помощью рассматриваемой схемы можно указывать границы положения искомой комбинации фраз на странице текста, ограничивать положение страниц с искомыми фразами и т.д.
, расстояние между символами, словами, предложениями. С помощью этих признаков можно организовать иерархию вложенных условий, применяя их заново к уже найденным фразам. Результат применения иерархически усложняющихся условий поиска – точная идентификация искомых фрагментов текста. При этом число вложений по построению схемы не ограничено. С помощью рассматриваемой схемы можно указывать границы положения искомой комбинации фраз на странице текста, ограничивать положение страниц с искомыми фразами и т.д.
Как отмечалось, имеет место взаимно однозначное индексное соответствие между искомыми фразами (словами, словосочетаниями, предложениями) и нулевыми элементами сопоставленного числового массива. Схема поиска текстовых фрагментов переносится на поиск файлов по заданным условиям поиска текстовых фрагментов произвольно заданного содержания среди группы текстовых файлов. Условия поиска могут иметь охарактеризованную ранее сложность. Рассматривается строковый массив, каждая строка которого – имя исследуемого файла в памяти компьютера. Задается условие, по которому должен идентифицироваться искомый файл. При этом на список имен файлов могут накладываться ограничения, идентичные ограничениям на строковые элементы. При последовательном обращении к каждому файлу, имя которого указано в строковом массиве, применяется описанная выше схема поиска внутри файла. Файл идентифицируется, если комбинация содержащихся в нем фраз удовлетворяет заданному условию.
Отличие данной схемы от известных в том, что она сводит поиск текстовых фрагментов к нахождению минимальных элементов числовой последовательности. Формально это дает возможность конструировать условие поиска в виде функционального, алгебраического и других уравнений, использовать в качестве условия поиска постановки математических задач. Другое, уже не формальное, отличие заключается в том, что предложенная схема совмещает текстовый поиск с поиском числовых значений в формате с плавающей точкой, при этом заданные значения можно находить не только по совпадению, но и с точностью до априори заданной границы абсолютной погрешности или же в заданном диапазоне. В дальнейшем на этой основе строится поиск фрагментов оцифрованных изображений, а также поиск неисправностей цифровых схем.
Описанный поиск может выполняться максимально параллельно по всем фрагментам текста и по всем сравнениям, требуемым сортировкой, при этом используемая модификация сортировки подсчетом обладает максимальным параллелизмом. В главе и в приложении к диссертации представлены программные реализации всех описанных выше схем, включая поиск чисел произвольного типа, поиск по комбинации символов в массиве строковых элементов, поиск текстовых фрагментов и файлов. Примеры поиска содержат полные коды разработанных программ.
Во второй главе разработанные в главе 1 схемы модифицируются для поиска одновременно по нескольким маскам с учетом изменяемости словоформ. Как и описанные ранее схемы, их видоизменения строятся на основе сортировки и идентификации экстремальных элементов последовательности чисел, сопоставленных просматриваемым текстовым фрагментам. Поиск сводится к программной идентификации всех локально экстремальных (в общем случае не обязательно нулевых) элементов данной последовательности. Известные поисковые системы реализуют поиск по произвольному числу масок, не детерминируя взаимное расположение масок в общем виде. Конструируемые в главе схемы свободны от данного ограничения. Они выполняют поиск одновременно по нескольким маскам, представляющим собой строковые элементы, априори указывая произвольно фиксированные расстояния между масками (взаимное расположение масок раскрыто в виде дополнительного условия поиска). Исходная схема строится следующим образом. Задается последовательность слов, принимаемых в качестве масок поиска, и порядок их взаимного расположения, неизменный до конца поиска. Исследуемая строка «нормируется» – удаляются все знаки препинания, между словами оставляется один пробел. Строка переводится в одномерный массив тех же слов с сохранением порядка. Массиву слов взаимно однозначно по номерам элементов сопоставляется одномерный числовой массив. Пусть число масок равно ![]() . На первом шаге алгоритма массив формируется из нулевых элементов, нумерация элементов начинается с единицы. Выбирается первая из
. На первом шаге алгоритма массив формируется из нулевых элементов, нумерация элементов начинается с единицы. Выбирается первая из ![]() масок. Просматривается сопоставленный строковый массив, начиная с номера
масок. Просматривается сопоставленный строковый массив, начиная с номера ![]() , для
, для ![]() –го слова этого массива проверяется совпадение с выбранной маской. В случае несовпадения к
–го слова этого массива проверяется совпадение с выбранной маской. В случае несовпадения к ![]() –му элементу числового массива прибавляется значение равное 1, иначе этот числовой элемент не меняется. Выполняется переход к
–му элементу числового массива прибавляется значение равное 1, иначе этот числовой элемент не меняется. Выполняется переход к ![]() -му слову, процесс продолжается для всех слов строкового массива при сравнении с первой маской. Затем процесс воспроизводится для второй и, аналогично, последующих масок.
-му слову, процесс продолжается для всех слов строкового массива при сравнении с первой маской. Затем процесс воспроизводится для второй и, аналогично, последующих масок.
Предложение 1. В результате ![]() проходов входному массиву слов взаимно однозначно по номерам элементов сопоставится числовой массив, значениями элементов которого являются либо
проходов входному массиву слов взаимно однозначно по номерам элементов сопоставится числовой массив, значениями элементов которого являются либо ![]() , либо
, либо ![]() . При этом числу
. При этом числу ![]() с единственностью индекса соответствует наличие во входном массиве строкового элемента, совпадающего с одним из
с единственностью индекса соответствует наличие во входном массиве строкового элемента, совпадающего с одним из ![]() значений маски.
значений маски.
Таким образом, поиск слов, совпадающих с заданными масками, сводится к поиску в числовом массиве значения ![]() . Этот поиск может осуществляться как поиск минимальных (по отношению к
. Этот поиск может осуществляться как поиск минимальных (по отношению к ![]() ) элементов, оператор локализации минимумов позволяет найти не только все строковые элементы, совпадающие с заданными масками, но и найти те из них, которые содержатся в заданной окрестности текущего индекса. В главе дано обобщение схемы на случай поиска по сходству с учетом изменяемости маски поиска, причем оператор локализации минимумов используется в качестве инструмента оценки меры сходства. Сопоставление числового массива происходит следующим образом. Задается эталон – искомое слово – и слова, которые имеют отличия от эталона. Каждому заданному слову ставится во взаимно однозначное соответствие число (вес), определяющее меру сходства. Эталону ставится в соответствие 0. Первому слову из допустимого набора (в количестве
) элементов, оператор локализации минимумов позволяет найти не только все строковые элементы, совпадающие с заданными масками, но и найти те из них, которые содержатся в заданной окрестности текущего индекса. В главе дано обобщение схемы на случай поиска по сходству с учетом изменяемости маски поиска, причем оператор локализации минимумов используется в качестве инструмента оценки меры сходства. Сопоставление числового массива происходит следующим образом. Задается эталон – искомое слово – и слова, которые имеют отличия от эталона. Каждому заданному слову ставится во взаимно однозначное соответствие число (вес), определяющее меру сходства. Эталону ставится в соответствие 0. Первому слову из допустимого набора (в количестве ![]() ) отличных от эталонного, ставится в соответствие 1, следующему отличному от эталона слову ставится в соответствие число 2 и т.д. Полное отсутствие допустимых отличий оценивается числом, заведомо большим выбранных весов. Весовые отличия определяются априори. Для сопоставления числового массива строка «нормируется» и переводится в массив, по ходу его просмотра
) отличных от эталонного, ставится в соответствие 1, следующему отличному от эталона слову ставится в соответствие число 2 и т.д. Полное отсутствие допустимых отличий оценивается числом, заведомо большим выбранных весов. Весовые отличия определяются априори. Для сопоставления числового массива строка «нормируется» и переводится в массив, по ходу его просмотра ![]() –е слово сравнивается с эталоном, начиная с
–е слово сравнивается с эталоном, начиная с ![]() , если оно полностью совпадает с эталоном, то i –му элементу числового массива ставится в соответствие число 0, иначе этому элементу ставится в соответствие число, определенное в качестве меры сходства (путем сравнения со словарем). В сопоставленном числовом массиве оператор локализации минимума идентифицирует все слова, совпадающие с эталонной маской поиска (значение 0), слова, сходные с маской (значения 1,2,…
, если оно полностью совпадает с эталоном, то i –му элементу числового массива ставится в соответствие число 0, иначе этому элементу ставится в соответствие число, определенное в качестве меры сходства (путем сравнения со словарем). В сопоставленном числовом массиве оператор локализации минимума идентифицирует все слова, совпадающие с эталонной маской поиска (значение 0), слова, сходные с маской (значения 1,2,… ![]() ). В этой схеме оператор локализации минимума используется уже по существу, как идентификатор значений экстремумов с указанием индексов, по которым идентифицируются искомые по мере сходства элементы и особенности их взаимного положения. Сохраняется возможность вложений рассмотренных схем при совпадении минимума с нулем (совпадение с эталоном) и при его совпадении с произвольно задаваемым весом (с точностью до заданной меры сходства). Предложенные схемы переносятся на поиск в текстовых файлах и поиск с учетом «опечаток». В последнем случае, если слово полностью совпадает с эталоном, то i –му элементу сопоставленного числового массива ставится в соответствие 0, если слово совпадает нечетко, то ему ставится в соответствие 1. Иначе этому элементу ставится в соответствие заведомо большое число:
). В этой схеме оператор локализации минимума используется уже по существу, как идентификатор значений экстремумов с указанием индексов, по которым идентифицируются искомые по мере сходства элементы и особенности их взаимного положения. Сохраняется возможность вложений рассмотренных схем при совпадении минимума с нулем (совпадение с эталоном) и при его совпадении с произвольно задаваемым весом (с точностью до заданной меры сходства). Предложенные схемы переносятся на поиск в текстовых файлах и поиск с учетом «опечаток». В последнем случае, если слово полностью совпадает с эталоном, то i –му элементу сопоставленного числового массива ставится в соответствие 0, если слово совпадает нечетко, то ему ставится в соответствие 1. Иначе этому элементу ставится в соответствие заведомо большое число:
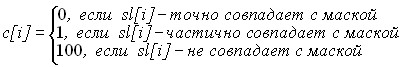 (4)
(4)
В результате исходной строке ставится во взаимно однозначное соответствие числовой массив, каждый элемент которого равен 0, 1 или 100. Оператор локализации минимумов определит все слова, совпадающие с эталоном (значение 0), слова, сходные с ним (значение 1). Индексы экстремумов позволят включить условие взаимного положения искомых слов. Для оценки нечеткого совпадения можно использовать известные способы. В главе дана схема поиска одновременно по нескольким маскам с априори указанным расстоянием между ними. Рассматривается фраза из ![]() слов и заданы
слов и заданы ![]() масок поиска, между словами, отвечающими 1-й и 2-й маскам, должно быть расположено
масок поиска, между словами, отвечающими 1-й и 2-й маскам, должно быть расположено ![]() слов, между словами, отвечающими 1-й и 3-й маскам, –
слов, между словами, отвечающими 1-й и 3-й маскам, –![]() слов, …, между словами, отвечающими 1-й и
слов, …, между словами, отвечающими 1-й и ![]() -ой маскам, –
-ой маскам, – ![]() слов. Первой маске поиска сопоставляется число
слов. Первой маске поиска сопоставляется число ![]() , второй –
, второй – ![]() ,…,
,…, ![]() -ой – число
-ой – число ![]() . Фразе, как и раньше в схеме поиска с учетом словоформ, ставится в соответствие числовой массив
. Фразе, как и раньше в схеме поиска с учетом словоформ, ставится в соответствие числовой массив ![]() из
из ![]() элементов. При каждом значении
элементов. При каждом значении ![]() , начиная с
, начиная с ![]() ,
, ![]() -му элементу массива
-му элементу массива ![]() сопоставляется элемент массива
сопоставляется элемент массива ![]() по соотношению:
по соотношению:
 . (5)
. (5)
По построению массива (5) элемент ![]() принимает нулевое значение в том и только в том случае, если для
принимает нулевое значение в том и только в том случае, если для ![]() -го слова существуют все заданные маски с априори заданным расстоянием: если
-го слова существуют все заданные маски с априори заданным расстоянием: если ![]() -му слову соответствует 1-я маска,
-му слову соответствует 1-я маска, ![]() -му слову – 2-я маска, …,
-му слову – 2-я маска, …, ![]() -му слову –
-му слову – ![]() –я маска, то, соответственно,
–я маска, то, соответственно, ![]() ,
, ![]() , …,
, …, ![]() . Отсюда
. Отсюда ![]() .
.
Таким образом, поиск группы слов с априори заданным расстоянием между ними сводится к поиску нулей в числовом массиве размерности ![]() .
.
В главе дана еще одна схема текстового поиска одновременно по нескольким маскам, которая отличается тем, что по идентифицированным индексам экстремумов без дополнительного просмотра окрестности локализованного значения и без сверки с масками дает однозначный ответ, какое именно слово было найдено. В дальнейшем именно эта схема будет преобразована для поиска объектов различных типов по нескольким свойствам. Схема строится следующим образом. Исследуемой строке сопоставляется (описываемым ниже способом) одномерный числовой массив, количество элементов которого совпадает с количеством слов заданной строки. Элементы сопоставленного числового массива, соответствующие различным маскам, перемножаются, причем сомножители априори задаются так, чтобы произведения взаимно однозначно соответствовали различным маскам, а локальные минимумы в их последовательности единственным образом соотносились с полным набором масок. Сопоставление массиву слов ![]() числового массива
числового массива ![]() выполняется по соотношениям:
выполняется по соотношениям:
 (6)
(6)
При этом индексы элементов ![]() совпадают с индексами элементов
совпадают с индексами элементов ![]() . К отсортированному массиву
. К отсортированному массиву ![]() применяется оператор локализации минимумов. Если локализация минимума выполняется в окрестности наперед заданного радиуса, не меньшего числа сгруппированных масок, то идентифицированным окажется искомое сочетание одновременно нескольких масок. Тем самым оказывается возможным вести поиск не по разрозненному сочетанию нескольких масок, а по их взаимосвязанному положению в исследуемом массиве слов. Схема формализуется следующим образом. Пусть
применяется оператор локализации минимумов. Если локализация минимума выполняется в окрестности наперед заданного радиуса, не меньшего числа сгруппированных масок, то идентифицированным окажется искомое сочетание одновременно нескольких масок. Тем самым оказывается возможным вести поиск не по разрозненному сочетанию нескольких масок, а по их взаимосвязанному положению в исследуемом массиве слов. Схема формализуется следующим образом. Пусть ![]() – номер текущего элемента исследуемого массива слов. Пусть
– номер текущего элемента исследуемого массива слов. Пусть ![]() – количество масок поиска и
– количество масок поиска и ![]() -му слову сопоставлено одно из двух значений
-му слову сопоставлено одно из двух значений ![]() и
и ![]() :
:
 (7)
(7)
При этом в (7) ![]() , если
, если ![]() -е слово совпадает с
-е слово совпадает с ![]() -й маской поиска,
-й маской поиска, ![]() , если
, если ![]() -е слово не совпадает с
-е слово не совпадает с ![]() -й маской поиска,
-й маской поиска, ![]() . Данные соотношения устанавливаются по ходу просмотра по всем
. Данные соотношения устанавливаются по ходу просмотра по всем ![]() с одним зафиксированным значением
с одним зафиксированным значением ![]() . Начальное значение
. Начальное значение ![]() принимается равным 1. При следующем просмотре значение
принимается равным 1. При следующем просмотре значение ![]() увеличивается на 1. Процесс продолжается до исчерпания значения всех
увеличивается на 1. Процесс продолжается до исчерпания значения всех ![]() масок поиска. С учетом (7)
масок поиска. С учетом (7)
 . (8)
. (8)
Данный способ формирования масок по соотношениям (6)-(8), или, что то же самое, по соотношению (6) будет именоваться мультипликативной схемой (6). Имеет место
Лемма 1. Пусть для заданных масок сформирован массив (6). Тогда при любом выборе элемента (6) значения произведений ![]() не совпадают при различных значениях индекса
не совпадают при различных значениях индекса ![]() из (8). Иными словами, при
из (8). Иными словами, при ![]() выполнено
выполнено ![]() в случае совпадения
в случае совпадения ![]() –го и
–го и ![]() –го слов массива
–го слов массива ![]() с какими бы то ни было соответственно различными масками из заданного набора.
с какими бы то ни было соответственно различными масками из заданного набора.
По лемме 1 значения ![]() взаимно однозначно соответствуют словам, совпадающим с масками. В данной схеме число масок произвольно. Значения
взаимно однозначно соответствуют словам, совпадающим с масками. В данной схеме число масок произвольно. Значения ![]() оказываются заведомо равны для тех номеров слов
оказываются заведомо равны для тех номеров слов ![]() , которые не совпадают ни с одной из масок (8). При этом данные значения
, которые не совпадают ни с одной из масок (8). При этом данные значения ![]() превосходят по величине значения, соответствующие словам, совпадающим с масками. Данную числовую схему определения признаков маски можно применить к любому наперед заданному числу масок путем подбора начального сомножителя факториального отрезка и конечного значения числового признака маски. Имеет место
превосходят по величине значения, соответствующие словам, совпадающим с масками. Данную числовую схему определения признаков маски можно применить к любому наперед заданному числу масок путем подбора начального сомножителя факториального отрезка и конечного значения числового признака маски. Имеет место
Теорема 1. Пусть количество масок, заданных в виде строковых элементов, равно ![]() и для них сконструировано соотношение (6). Тогда оператор локализации минимума в окрестности радиуса
и для них сконструировано соотношение (6). Тогда оператор локализации минимума в окрестности радиуса ![]() идентифицирует все локально минимальные элементы, соответствующие группе из
идентифицирует все локально минимальные элементы, соответствующие группе из ![]() подряд расположенных масок.
подряд расположенных масок.
В главе обсуждаются варианты поиска, основанные на теореме 1 и следствиях из нее. Мультипликативная схема поиска в массиве слов или в отдельной фразе переносится на поиск в текстовых файлах. Числовые идентификаторы, по которым локализуются значения, могут быть рассчитаны наперед. Поэтому анализ результатов поиска может вестись по совпадению с такими числовыми значениями в локализованной окрестности. Для упрощения анализа эти числовые значения могут быть упорядочены с помощью сортировки, тогда анализ можно проводить до первого несовпадения числовых значений.
Если условием поиска является не только определение местоположения заданных слов, сгруппированных воедино, но и наличия в группе заданного порядка слов, то радиус ![]() при задании условия следует считать равным числу масок группы. При этом оказывается, что при выполнении условия числовые элементы искомой группы и их индексы будут упорядочены по возрастанию, а индексы соседних элементов монотонно возрастают на единицу. Имеет место
при задании условия следует считать равным числу масок группы. При этом оказывается, что при выполнении условия числовые элементы искомой группы и их индексы будут упорядочены по возрастанию, а индексы соседних элементов монотонно возрастают на единицу. Имеет место
Теорема 2. Если в условиях леммы 1 ![]() -е слово соответствует
-е слово соответствует ![]() -ой маске поиска, а
-ой маске поиска, а ![]() -е слово соответствует
-е слово соответствует ![]() -ой маске поиска, то
-ой маске поиска, то ![]() .
.
Таким образом, при выполнении условия поиска индекс локализованного значения всегда наименьший, последующие индексы упорядочены, количество элементов в локализованной окрестности, отвечающих рассматриваемой сгруппированной маске, совпадает с количеством заданных масок. Отсюда вытекает
Следствие 1. В условиях теоремы 2 поиск по группе упорядоченных масок всегда можно выполнять с помощью оператора локализации минимума в ![]() -окрестности, где
-окрестности, где ![]() равно числу масок группы, при этом в окрестности минимума индексы располагаются в порядке возрастания без пропусков.
равно числу масок группы, при этом в окрестности минимума индексы располагаются в порядке возрастания без пропусков.
В развитие методов первой главы даны несколько способов формирования числовой последовательности, взаимно однозначно соответствующей объектам поиска в тексте. На этой основе построены схемы идентификации экстремальных элементов последовательности, по которым осуществляется поиск по группам одновременно нескольких масок с учетом их взаимного сочетания и расположения. Схемы позволяют выполнять поиск одновременно по нескольким маскам с учетом их взаимной зависимости, а также взаимного расположения полных и частичных комбинаций заданных масок. Разработана модификация мультипликативной схемы на случай поиска по нескольким маскам с учетом изменяемости их словоформ, которая в отличие от существующих схем учитывает не только различные словоформы масок, но и их взаимное расположение.
Предложенные схемы поиска отличаются от известных схем по построению на основе сортировки и оператора локализации минимумов, при этом поиск сводится к задаче безусловной оптимизации в сопоставленной числовой последовательности. Отличие, кроме того, заключается в том, что схемы дают детерминированный результат поиска одновременно по нескольким маскам с учетом их взаимного положения, а также с учетом взаимного положения их частичных комбинаций и словоформ.
В главе и в приложении к диссертации представлены программные реализации (с полными кодами программ) поиска по всем описанным выше схемам, включая поиск по нескольким маскам с учетом изменяемости словоформ и их взаимного расположения.
В третьей главе мультипликативная схема поиска модифицируется с целью применения к поиску объектов различных типов. Кроме того, схема видоизменяется для идентификации заданных свойств объектов. Модифицированная схема строится на исходной основе сортировки и идентификации экстремальных элементов числовой последовательности, сопоставленной исследуемому множеству объектов. Однако, сопоставление (первоначально только тексту) одномерного числового массива без изменения конечного результата выполняется иначе, чем это было сделано в главе 2. Пусть дан массив ![]() из
из ![]() слов, в котором требуется выполнить поиск по заданной последовательности
слов, в котором требуется выполнить поиск по заданной последовательности ![]() масок
масок ![]() , расположенных в определенном и фиксированном порядке. На первом шаге массиву
, расположенных в определенном и фиксированном порядке. На первом шаге массиву ![]() сопоставляется двумерный числовой массив
сопоставляется двумерный числовой массив ![]() :
:
 (9)
(9)
В (9) и ниже ![]() ,
, ![]() . На основе (9) формируется промежуточный двумерный массив
. На основе (9) формируется промежуточный двумерный массив ![]() :
:
 (10)
(10)
Затем путем перемножения элементов столбцов (10) формируется одномерный массив ![]() :
:
![]() (11)
(11)
Данным приемом любой массив, состоящий из нулей и единиц, переводится в одномерный числовой массив, где при каждом ![]() исследуемому объекту (слову) с номером
исследуемому объекту (слову) с номером ![]() соответствует
соответствует ![]() -й столбец массива
-й столбец массива ![]() , в котором не более одного единичного значения. При этом несущественно, какова природа рассматриваемых объектов. Поэтому ниже данная конструкция используется не для поиска строковых элементов, а для идентификации объектов одновременно различных типов или, в более общем случае, объектов, характеризуемых свойствами различной природы. Непосредственно ниже, для определенности, идет речь об объектах не обязательно текстового типа, но все объекты рассматриваемого множества должны иметь один и тот же тип. В дальнейшем это условие не будет обязательным, будут рассмотрены объекты с признаками множественной природы. Вначале конструируется поиск объекта из упорядоченного множества по группе признаков, заданных в фиксированном порядке. При этом признаки и объекты могут быть произвольно фиксированного типа или характеризоваться произвольно фиксированным свойством. Ограничение заключается в том, что каждый объект может соответствовать одному и не более чем одному признаку. В конструируемой схеме заполнение соответствующих массивов
, в котором не более одного единичного значения. При этом несущественно, какова природа рассматриваемых объектов. Поэтому ниже данная конструкция используется не для поиска строковых элементов, а для идентификации объектов одновременно различных типов или, в более общем случае, объектов, характеризуемых свойствами различной природы. Непосредственно ниже, для определенности, идет речь об объектах не обязательно текстового типа, но все объекты рассматриваемого множества должны иметь один и тот же тип. В дальнейшем это условие не будет обязательным, будут рассмотрены объекты с признаками множественной природы. Вначале конструируется поиск объекта из упорядоченного множества по группе признаков, заданных в фиксированном порядке. При этом признаки и объекты могут быть произвольно фиксированного типа или характеризоваться произвольно фиксированным свойством. Ограничение заключается в том, что каждый объект может соответствовать одному и не более чем одному признаку. В конструируемой схеме заполнение соответствующих массивов ![]() и
и ![]() ведется с помощью проверки соответствия или несоответствия исследуемого объекта заданному признаку согласно (9), (10), где наличие (отсутствие) соответствия кодируется единицей (нулем) так же, как кодировалось совпадение (несовпадение) с маской, проверка выполняется при фиксированном порядке обхода объектов. После сортировки массива
ведется с помощью проверки соответствия или несоответствия исследуемого объекта заданному признаку согласно (9), (10), где наличие (отсутствие) соответствия кодируется единицей (нулем) так же, как кодировалось совпадение (несовпадение) с маской, проверка выполняется при фиксированном порядке обхода объектов. После сортировки массива ![]() из (11) применяется оператор локализации минимумов, который по наличию локальных числовых минимумов идентифицирует индексы искомых объектов так, как раньше он идентифицировал индексы слов, совпадающих с масками поиска. По идентифицированным индексам на основе совпадения индексов числового массива и массива исходных объектов выполняется переход от числовых экстремумов к искомым объектам в исходном виде. Непосредственно ниже этот подход видоизменяется для поиска объекта с одновременно несколькими его признаками.
из (11) применяется оператор локализации минимумов, который по наличию локальных числовых минимумов идентифицирует индексы искомых объектов так, как раньше он идентифицировал индексы слов, совпадающих с масками поиска. По идентифицированным индексам на основе совпадения индексов числового массива и массива исходных объектов выполняется переход от числовых экстремумов к искомым объектам в исходном виде. Непосредственно ниже этот подход видоизменяется для поиска объекта с одновременно несколькими его признаками.
Согласно (9) - (11) каждому исследуемому объекту сопоставляется единственное число. В случае если объект обладает одновременно несколькими искомыми свойствами, эта единственность нарушается. Требуется модифицировать схему, чтобы каждому объекту с заданным набором признаков числовое значение сопоставлялось единственным образом. Пусть дано проиндексированное множество ![]() из
из ![]() однотипных объектов, в котором требуется выполнить поиск по заданной последовательности признаков
однотипных объектов, в котором требуется выполнить поиск по заданной последовательности признаков ![]() , расположенных в определенном и фиксированном порядке. Пусть число признаков равно
, расположенных в определенном и фиксированном порядке. Пусть число признаков равно ![]() . Как и прежде, формируются массивы mass, mass1 и
. Как и прежде, формируются массивы mass, mass1 и ![]() , но при этом (10) заменяется на следующее соотношение:
, но при этом (10) заменяется на следующее соотношение:
 (12)
(12)
где ![]() - конечная последовательность из
- конечная последовательность из ![]() упорядоченных простых чисел
упорядоченных простых чисел ![]() . Имеет место взаимно однозначное соответствие между набором признаков, присущих исследуемому объекту
. Имеет место взаимно однозначное соответствие между набором признаков, присущих исследуемому объекту ![]() , и сопоставленным числовым значением
, и сопоставленным числовым значением ![]() : значение
: значение ![]() по теореме о простых числах единственным образом разложимо на простые множители, по этому разложению данное число обратимо указывает на те признаки (9), которыми обладает объект соответственно простым сомножителям
по теореме о простых числах единственным образом разложимо на простые множители, по этому разложению данное число обратимо указывает на те признаки (9), которыми обладает объект соответственно простым сомножителям ![]() из (12). Обратно, каждому набору признаков, присущих объекту, в силу той же теоремы и по построению (9), (11), (12) соответствует единственное значение произведения элементов столбца, образующее элемент сопоставленной числовой последовательности (11). Числовые идентификаторы наборов признаков (при полном и частичном совпадении) могут быть априори рассчитаны, на этой основе выполняется поиск не только по полному набору заданных свойств, но и по их частичному набору. Путем анализа окрестности локализованных минимумов можно, помимо того, выполнить поиск не только одного объекта, но и группы таких объектов по нескольким признакам одновременно.
из (12). Обратно, каждому набору признаков, присущих объекту, в силу той же теоремы и по построению (9), (11), (12) соответствует единственное значение произведения элементов столбца, образующее элемент сопоставленной числовой последовательности (11). Числовые идентификаторы наборов признаков (при полном и частичном совпадении) могут быть априори рассчитаны, на этой основе выполняется поиск не только по полному набору заданных свойств, но и по их частичному набору. Путем анализа окрестности локализованных минимумов можно, помимо того, выполнить поиск не только одного объекта, но и группы таких объектов по нескольким признакам одновременно.
Мультипликативную схему в форме (9), (11), (12) можно адаптировать к поиску группы объектов, типы которых различны между собой. В качестве примера можно взять поиск каталога, содержащего файлы различных типов. Каталог рассматривается как объект исследования, а наличие требуемого файла в исследуемом каталоге – как признак поиска. Каталог с такими признаками идентифицируется по мультипликативной схеме (9), (11), (12). При анализе каталога для каждого файла из этого каталога описанная ранее схема поиска без изменения применима к файлам различного типа в том случае, если типы объектов совместимы или могут быть приведены к одному типу в операционной системе, например, *.txt, *.dpr, *.pas, *.xls, *.doc. Для реализации поиска объектов, которые не приводятся к одному и тому же типу, например, *.dat, *. bmp предлагается описываемая в дальнейшем специальная схема.
Для поиска на рассматриваемой основе файлов, содержащих разнотипные данные внутри файла, включая данные текстового типа, рисунки в формате *.bmp, числа с плавающей точкой, программные коды в различных языках программирования, можно поступить следующим образом. Исследуемому файлу сопоставляется группа файлов, например, текстовый файл *.txt, непосредственно содержащий текст исследуемого файла, графические файлы *.bmp, содержащие внедренные в исследуемый файл рисунки, типизированный файл *.dat, который содержит все числовые значения, присутствующие в данном файле и т.д. Поиск в исходном файле в результате сводится к поиску в файлах сопоставленной группы. Каждая группа рассматривается как объект со многими признаками поиска, а наличие или отсутствие в объекте файла, соответствующего маске поиска, как признак объекта для его идентификации. Таким образом, используется рекуррентное вложение схем поиска. Объединенный результат поиска можно получить по схеме с использованием (9), (11), (12), что позволяет свести поиск к идентификации локальных экстремумов числовой последовательности и в этом сравнительно общем случае.
Поиск в файлах *.dat искомого числового значения с точностью до ![]() можно выполнить на основе схемы поиска элемента в числовом массиве с заданной границей погрешности. Информация из типизированного числового файла считывается в числовой массив с сохранением порядка следования элементов. Далее без изменений применяется схема, описанная в главе 1. Схема обобщается на поиск самих типизированных числовых файлов по признаку наличия в нем заданного числового значения с допустимой границей точности. С целью поиска файлов типа *.bmp каждому файлу (предполагается, что файл содержит только один рисунок) сопоставляется вектор распознавания. Этот вектор можно сформировать на основе какой-либо известной схемы. В главе показано (как поясняется ниже), что вектор распознавания может быть сформирован с использованием мультипликативной схемы. Если вектор сформирован, то для текущего рисунка находится норма разности между вектором исследуемого рисунка и эталонным вектором. Рисунок считается найденным, если норма разности соответственной пары векторов не превосходит заданной границы погрешности. Мультипликативная схема (9), (11), (12) может следующим образом применяться для формирования векторов распознавания при поиске растровых двуцветных изображений. Первоначально рассматриваются плоские изображения, для определенности размера
можно выполнить на основе схемы поиска элемента в числовом массиве с заданной границей погрешности. Информация из типизированного числового файла считывается в числовой массив с сохранением порядка следования элементов. Далее без изменений применяется схема, описанная в главе 1. Схема обобщается на поиск самих типизированных числовых файлов по признаку наличия в нем заданного числового значения с допустимой границей точности. С целью поиска файлов типа *.bmp каждому файлу (предполагается, что файл содержит только один рисунок) сопоставляется вектор распознавания. Этот вектор можно сформировать на основе какой-либо известной схемы. В главе показано (как поясняется ниже), что вектор распознавания может быть сформирован с использованием мультипликативной схемы. Если вектор сформирован, то для текущего рисунка находится норма разности между вектором исследуемого рисунка и эталонным вектором. Рисунок считается найденным, если норма разности соответственной пары векторов не превосходит заданной границы погрешности. Мультипликативная схема (9), (11), (12) может следующим образом применяться для формирования векторов распознавания при поиске растровых двуцветных изображений. Первоначально рассматриваются плоские изображения, для определенности размера ![]() пикселей, в растровом формате BMP. Изображению сопоставляется двумерная числовая матрица
пикселей, в растровом формате BMP. Изображению сопоставляется двумерная числовая матрица ![]() ,
, ![]() , каждый элемент которой принимает только два значения: 0 или 1. Значением 0 кодируется белый цвет, значением 1 – черный. Полученной матрице
, каждый элемент которой принимает только два значения: 0 или 1. Значением 0 кодируется белый цвет, значением 1 – черный. Полученной матрице ![]() согласно (11), (12) сопоставляется двумерный массив
согласно (11), (12) сопоставляется двумерный массив ![]() и одномерный числовой массив
и одномерный числовой массив ![]() . Элемент этого массива с номером
. Элемент этого массива с номером ![]() образуется как произведение простых чисел столбца с тем же номером из матрицы
образуется как произведение простых чисел столбца с тем же номером из матрицы ![]() . Таким образом, по отношению к матрице из нулей и единиц, кодирующей исходное двуцветное изображение, полностью воспроизводится алгоритм (11), (12) сопоставления числовой последовательности, который ранее применялся для поиска по отношению к матрице
. Таким образом, по отношению к матрице из нулей и единиц, кодирующей исходное двуцветное изображение, полностью воспроизводится алгоритм (11), (12) сопоставления числовой последовательности, который ранее применялся для поиска по отношению к матрице ![]() из (9). Данное приложение алгоритма позволяет сформировать для каждого рисунка вектор распознавания в виде массива
из (9). Данное приложение алгоритма позволяет сформировать для каждого рисунка вектор распознавания в виде массива ![]() из (11) и с его помощью решить две задачи: поиск плоских двуцветных изображений и распознавание плоских двуцветных изображений с помощью сопоставленного вектора. При данном подходе изображение может быть идентифицировано вектором, роль которого играет массив
из (11) и с его помощью решить две задачи: поиск плоских двуцветных изображений и распознавание плоских двуцветных изображений с помощью сопоставленного вектора. При данном подходе изображение может быть идентифицировано вектором, роль которого играет массив ![]() . Набор таких векторов может храниться в виде эталонов, с которыми по соответственному выходному массиву
. Набор таких векторов может храниться в виде эталонов, с которыми по соответственному выходному массиву ![]() сравниваются искомые объекты. Такая схема поиска переходит в способ распознавания, отличающийся двумя аспектами. Первый из них заключается в построении, второй – в том, что распознавание получается обратимым преобразованием матрицы изображения
сравниваются искомые объекты. Такая схема поиска переходит в способ распознавания, отличающийся двумя аспектами. Первый из них заключается в построении, второй – в том, что распознавание получается обратимым преобразованием матрицы изображения ![]() в вектор размерности
в вектор размерности ![]() , который интерпретируется как вектор распознавания.
, который интерпретируется как вектор распознавания.
В главе обоснованы следующие утверждения.
Предложение 2. Массив ![]() единственным образом идентифицирует изображение.
единственным образом идентифицирует изображение.
Следствие 2. Описанное преобразование изображения обратимо.
Пример формирования вектора распознавания для символа «»
| Матрица пикселей (массив | Массив простых чисел | Вектор распознавания | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Рис. 1.
Весьма существенна возможность преобразования размера базы эталонов и дополнительного сжатия изображения за счет замены вектора распознавания идентификаторами его глобального экстремума или набором идентификаторов локальных экстремумов. Второй из таких векторов ниже называется вектором локальных экстремумов. Такое сжатие не является обратимым. Тем не менее, распознавание изображения можно выполнить по вектору локальных экстремумов с привлечением дополнительных операций. Изложенная схема обобщается на изображения произвольного конечного размера.
В главе и в приложении к диссертации представлены программные реализации поиска по представленным вариантам мультипликативных схем, включая поиск объектов различных типов, программные реализации сжатия. Даны примеры поиска каталогов с файлами, включающими изображения, идентификации изображений с приведением полных кодов разработанных программ.
Представленный пример поиска данных различных типов включает поиск двуцветных изображений, распознавание изображения, его перевод в вектор, на основе которого можно идентифицировать изображение в силу обратимости алгоритма перевода. С некоторыми ограничениями схема распространяется на поиск числовых, формульных, текстовых фрагментов и данных других типов. По построению изложенный подход обобщается на поиск объектов одновременно нескольких произвольных типов, если эти типы реализованы в языке программирования.
Иллюстрируя возможность идентификации объектов произвольной природы, с оговоркой, что их природа идентифицируема в цифровом представлении, отметим, что по предложенной схеме идентифицируются цветные растровые изображения, матричные представления графов, разновидности логических функций по таблицам истинности и объекты других предметных областей. В диссертации приводятся примеры такой программной идентификации. Достаточным условием идентификации является выполнимость кодирования по схеме (9), (11), (12) тех свойств, по которым требуется выполнить поиск или распознавание. В главе даны примеры приложения метода к поиску объектов в изображении гербария, к распознаванию диагностических экстремальных особенностей электрокардиограмм, к распознаванию отпечатков пальцев. Применимость схемы (9), (11), (12) к идентификации логических функций позволяет перенести ее на случай тестирования логических и цифровых устройств. При этом объекты должны иметь фиксированный порядок взаимного расположения до конца процесса рассматриваемой обработки. В главе даны конкретные схемы и алгоритмы с формализованным описанием.
С целью тестирования логическое устройство рассматривается как упорядоченная последовательность составляющих его логических элементов. Логический элемент, в свою очередь, интерпретируется как логическая функция, которую он реализует. Возникает возможность свести тестирующую схему к идентификации логических функций и, соответственно, к проверке правильности функционирования элементов устройства. При этом априори просчитываются все экстремальные значения выходной последовательности модифицированной мультипликативной схемы (9), (11), (12) для правильного получения эталонных значений. Отклонения от эталонных значений экстремумов интерпретируются как ошибки функционирования. Полнота совпадения с эталонами интерпретируется как критерий правильности работы тестируемой схемы. С использованием обратимости схемы (9), (11), (12) можно идентифицировать сбойные элементы исследуемой схемы. В главе дан пример проверки исправности набора логических элементов схемы с помощью сопоставленной числовой последовательности ![]() из (11). Полная оценка исправности устройства может выполняться по сравнению последовательности
из (11). Полная оценка исправности устройства может выполняться по сравнению последовательности ![]() с эталонными последовательностями, частичная – может опираться на сравнение только с экстремальными элементами этих последовательностей.
с эталонными последовательностями, частичная – может опираться на сравнение только с экстремальными элементами этих последовательностей.
Особенностью предложенных схем поиска и идентификации объектов является их распараллеливаемость. Параллелизм основан на максимальной параллельности используемых сортировок, на естественном параллелизме обработки отдельно взятых файлов и их фрагментов. В главе приводится оценка временной сложности максимально параллельного поиска по мультипликативной схеме, которая в пределе достигает значения ![]() .
.
В заключении главы 3 дана таблица сравнения с возможностями известных поисковых систем, на основе которой утверждается, что предложенный подход расширяет их функциональные возможности.
В приложении приводятся листинги программ, излагается способ совмещения мультипликативной схемы поиска с известными методами, включая метод инвертированных сигнатурных файлов, обсуждается применение предложенного подхода для выполнения семантического поиска. При этом выполнение запроса в семантическом смысле обеспечивается на основе известных способов оценки семантического соответствия таким образом, что глобальный экстремум сопоставленной числовой последовательности идентифицирует совокупность фраз или текстов, одновременно содержащих все основные требования запроса в семантическом смысле.
Приложение включает также акты о внедрении результатов диссертационной работы.
В заключении обобщаются основные результаты диссертационной работы, характеризуется их научная новизна, отмечается практическая значимость проведенных исследований.
Основной результат диссертационной работы заключается в разработке и исследовании единой схемы применения сортировки в качестве базового конструктивного алгоритма текстового поиска, поиска объектов различных типов, распознавания и идентификации объектов одновременно по нескольким разнотипным признакам, в том числе, распознавания, идентификации и сжатия растровых изображений.
Работа включает следующие научные результаты.
- Сконструирован распараллеливаемый метод применения сортировки для поиска на ее основе локально экстремальных элементов числовой последовательности. Метод применяется с использованием кодовой таблицы символов для детерминированного поиска строковых элемен
тов, слов и словосочетаний в тексте, а также для обнаружения скрытых закономерностей плохо структурированного текста.
- Сконструирована схема с использованием обработки числовых выражений для поиска данных строкового и вещественного типа на основе подстановки индексов отсортированных элементов.
- Синтезирована схема детерминированного поиска одновременно по нескольким маскам с учетом комбинирования взаимного расположения масок и изменяемости словоформ, предложено ее видоизменение для поиска текстовых файлов по совокупности масок с заданным взаимным расположением.
- Доказаны теоремы, математически обосновывающие методы поиска. Показано, что в мультипликативной схеме поиска сопоставление элементов числовой последовательности производится с взаимно однозначным соответствием маскам поиска, где число масок произвольно. Поиск по сгруппированным в заданном порядке маскам выполняется с помощью оператора локализации минимума сопоставленной числовой последовательности, который в окрестности радиуса
 идентифицирует все локально минимальные элементы, соответствующие группе из
идентифицирует все локально минимальные элементы, соответствующие группе из  подряд расположенных масок.
подряд расположенных масок. - Разработана схема поиска конечного множества объектов различных типов, включая разнотипные файлы и оцифрованные объекты общего вида, на основе формализации признаков.
- Представлено преобразование основной схемы поиска для распознавания, идентификации и сжатия плоских оцифрованных изображений.
- На основе преобразования схемы поиска и идентификации разнотипных объектов синтезирован распараллеливаемый алгоритм идентификации неисправностей цифровых устройств.
ОСНОВНЫЕ ПУБЛИКАЦИИ ПО ТЕМЕ РАБОТЫ
- Ромм Я.Е., Белоконова С.С. Поиск и распознавание текстовых фрагментов на основе адресной сортировки и локализации экстремальных значений asc-кодов / ТГПИ. – Таганрог, 2001. – 22 с. Деп. в ВИНИТИ от 06.12.2001, № 2537 – В2001. (лично автора – 0,75 п.л.)
- Ромм Я.Е., Белоконова С.С. Схема поиска на основе сортировки и локализации экстремальных элементов / ТГПИ. – Таганрог, 2003. – 31 с. Деп. в ВИНИТИ 12.03.2003, № 436-В2003 (лично автора – 1 п.л.)
- Ромм Я.Е., Белоконова С.С. Применение сортировки и локализации экстремальных элементов к поиску. – В кн.: Сборник материалов 1-й международной научно-практической конференции 15-17 сентября 2003 г. под ред. А.К. Юрова. – Таганрог. –2003. – С. 100-105. (лично автора – 0,08 п.л.)
- Ромм Я.Е., Белоконова С.С. Схема поиска на основе сортировки и локализации экстремальных элементов. – В кн.: Сборник научных трудов 9-й международной конференции «Математические модели физических процессов». – Таганрог, ТГПИ. – 2003. – С. 100 – 103. (лично автора – 0,15 п.л.)
- Ромм Я.Е., Гуревич М.Ю., Белоконова С.С., Соловьёва И.А. Вычисление нулей и полюсов функций на основе устойчивой адресной сортировки с приложением к поиску и распознаванию // Проблемы программирования. – 2004. – №2-3. – С. 462–472. (лично автора – 0,36 п.л.)
- Ромм Я.Е., Белоконова С.С. Схема поиска и распознавания на основе идентификации экстремумов с помощью сортировки. – В кн.: Сборник научных трудов 10-й международной конференции «Математические модели физических процессов». – Таганрог, ТГПИ. – 2004. – С. 167 – 172. (лично автора – 0,2 п.л.)
- Ромм Я.Е., Белоконова С.С. Метод поиска на основе адресной сортировки и идентификации экстремумов в приложении к распознаванию / ТГПИ. – Таганрог, 2004. – 46 с. Деп. в ВИНИТИ от 05.08.2004. №1361-В2004. (лично автора – 1,4 п.л.)
- Ромм Я.Е., Белоконова С.С. Поиск по произвольному количеству масок на основе локализации экстремумов при помощи сортировки. – В кн.: Модернизация отечественного педагогического образования: проблемы, подходы, решения: Сб. науч. тр. Ч. II. «Технологические основы образовательного процесса в современной высшей школе. – Таганрог. –2005. – С. 24-29. (лично автора – 0,2 п.л.)
- Ромм Я.Е., Белоконова С.С. Схема поиска текста на основе локализации экстремумов при помощи сортировки. – В кн.: Материалы международной научной конференции «Оптимальные методы решения научных и практических задач» - часть 2 – Таганрог: Изд-во»Антон», ТРТУ, 2005. – С. 58-63. (лично автора – 0,2 п.л.)
- Ромм Я.Е., Белоконова С.С. Поиск по группам масок на основе сортировки и локализации экстремальных элементов / ТГПИ. – Таганрог, 2005. – 56 с. Деп. в ВИНИТИ от 28.06.05, № 916 – В2005. (лично автора – 1,5 п.л.)
- Ромм Я.Е., Белоконова С.С. Схема поиска данных различных типов по нескольким маскам на основе сортировки // Известия вузов. Северо-Кавказский регион. Техн. науки. Специальный выпуск «Математическое моделирование и компьютерные технологии», 2006. – С. 3 – 8. (лично автора – 0,4 п.л.)
- Ромм Я.Е., Белоконова С.С. Совмещение схемы поиска на основе сортировки с идентификацией двуцветных изображений. – В кн.: Материалы Международной научно-технической конференции «ММА-2006». – «Математические модели и алгоритмы для имитациифизических процессов». Т 1. Физико-математические и физико-технические модели и алгоритмы для имитациифизических процессов. – Таганрог. –2006. – С. 329 – 333. (лично автора – 0,2 п.л.)
- Белоконова С.С. Схема текстового поиска с учетом словоизменяемости на основе сортировки. – В кн.: Материалы Международной научно-технической конференции «ММА-2006». – «Математические модели и алгоритмы для имитациифизических процессов». Т 1. Физико-математические и физико-технические модели и алгоритмы для имитациифизических процессов. – Таганрог. –2006. – С. 333 – 336.
- Ромм Я.Е., Белоконова С.С. Схемы поиска данных различных типов по m маскам. – В кн.: Информационные технологии в образовании и консультационной деятельности в сельскохозяйственном производстве. – Новочеркасск. – 2006. – С. 164 – 171. (лично автора – 0,2 п.л.)
| Соискатель | Белоконова С.С. |
Подписано к печати Объем 1,1 уч.-изд.л.
Заказ Тираж 100 экз.

