6f> ov- syss/D
W. _*-* **
уральский государственный технический университет - упи
На правах рукописи
МОСИН Александр Михайлович
ОПТИМАЛЬНОЕ ПРОЕКТИРОВАНИЕ УПРУГОДЕФОРМИРУЕМЫХ
СТАЛЬНЫХ ПОРТАЛЬНЫХ РАМ С ЭЛЕМЕНТАМИ ПЕРЕМЕННОЙ
ЖЕСТКОСТИ НА ОСНОВЕ ГЕНЕТИЧЕСКОГО АЛГОРИТМА
05.23.01 - Строительные конструкции, здания и сооружения
Диссертация на соискание ученой степени кандидата технических наук
Научный руководитель
кандидат технических наук,
доцент В.Н.Алёхин
Екатеринбург - 2004
2 ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ 5
Глава 1. ОБЗОР МЕТОДОВ РАСЧЕТА И ОПТИМАЛЬНОГО
ПРОЕКТИРОВАНИЯ РАМНЫХ МЕТАЛЛОКОНСТРУКЦИЙ. 8
- Обзор методов расчета рамных металлоконструкций 8
- Обзор методов оптимизации рамных металлоконструкций 12
Выводы к главе 1 26
Глава 2. СТАТИЧЕСКИЙ РАСЧЕТ УПРУГОДЕФОРМИРУЕМЫХ СТАЛЬНЫХ
ПОРТАЛЬНЫХ РАМ С ЭЛЕМЕНТАМИ ПЕРЕМЕННОЙ ЖЕСТКОСТИ...28
- Основные предпосылки и допущения. Формирование расчетной схемы 28
- Вычисление элементов матрицы жесткости стержня переменного сечения 33
- Применение численного интегрирования. Линейная аппроксимация функции изменения жесткости стержня 34
- Использование степенной функции. 35
2.3. Моделирование эксцентрично-соединенных стержней при расчете
стержневой конструкции методом конечных элементов в форме метода
, перемещений. 36
- Вычисление матрицы жесткости стержневого суперэлемента 42
- Бинарно-суперэлементное представление стержневой расчетной схемы 45
- Статический расчет рамы с использованием МКЭ 48
- Статический расчет стальной портальной рамы с учетом геометрической нелинейности 50
Выводы к главе 2 57
Глава З.ОПРЕДЕЛЕНИЕ КРИТИЧЕСКОЙ НАГРУЗКИ НА ПОРТАЛЬНУЮ РАМУ
С ЭЛЕМЕНТАМИ ПЕРЕМЕННОЙ ЖЕСТКОСТИ ПРИ РАСЧЕТЕ НА
УСТОЙЧИВОСТЬ 58
3
3.1. Решения дифференциального уравнения сжато-изогнутой оси упругого
стержня для случая постоянной изгибной жесткости 59
- Решение в виде тригонометрической функции 59
- Решение в форме бесконечного ряда. 60
3.2. Приближенные решения дифференциального уравнения сжато-
изогнутой оси упругого стержня переменной жесткости 63
- Решение в виде бесконечного ряда 63
- Решение путем аппроксимации — замены стержня с жесткостью непрерывного изменения стержнем, составленным из отрезков стержней постоянной жесткости 65
3.2.3. Решение с использованием степенных функций 67
3.3.Определение критической нагрузки на раму с элементами переменного
сечения при расчете на устойчивость 70
ЗАОпределение верхнего предела критической нагрузки при расчете на
устойчивость рамы с элементами переменного сечения 72
Выводы к главе 3. 77
Глава 4 АЛГОРИТМ ОПТИМАЛЬНОГО ПРОЕКТИРОВАНИЯ СТАЛЬНЫХ
ПОРТАЛЬНЫХ РАМ С ЭЛЕМЕНТАМИ ПЕРЕМЕННОЙ ЖЕСТКОСТИ..78
- Генетические алгоритмы и их использование для оптимизации строительных конструкций 78
- Алгоритм оптимального проектирования стальных портальных рам
с элементами переменной жесткости 82
- Кодирование значений проектных параметров в виде двоичной строки. 91
- Требования по прочности, жесткости и другие проектные ограничения в алгоритме оптимизации стальных портальных рам 94
- Поясные листы (полки) центрально-, внецентренно-сжатых, сжато-изгибаемых и изгибаемых элементов переменного сечения..'. 94
- Проверка устойчивости внецентренно-сжатых элементов 95
- Требования по проектированию перфорированных балок. 96
4
4.5. Численный эксперимент и примеры использования разработанного
алгоритма 97
Выводы к главе 4 108
Основные результаты и выводы 109
Литература ПО
Приложение 1 122
Приложение II 130
5 ВВЕДЕНИЕ
Актуальность темы. Стальные портальные рамы представляют собой одно из распространенных проектных решений каркасов одноэтажных промышленных зданий. Практикой проектирования стальных рам показано, что применение элементов переменного сечения обеспечивает получение более экономичных решений в сравнении с использованием элементов постоянного сечения.
Достижения в области вычислительной техники и использование методов оптимального проектирования позволяют получать оптимальные или близкие к оптимальным решения некоторых задач оптимизации строительных конструкций. Одним из основных условий при проектировании оптимальных конструкций является выявление и обоснованное использование резервов несущей способности уже на стадии формирования расчетной модели. В связи с этим немалую актуальность приобретает применение уточненных расчетных моделей, в том числе, позволяющих учитывать физическую и геометрическую нелинейности.
Диссертационная работа посвящена разработке алгоритма оптимизации стальных портальных рам с элементами переменного сечения по критерию минимума массы конструкции с включением в число проектных параметров координат узлов стыка элементов ригеля. Алгоритм разрабатывается на основе расчета конструкции методом конечных элементов и постановки задачи оптимизации в форме генетического алгоритма. Учет геометрической нелинейности выполняется с использованием метода Ньютона-Рафсона.
Целью исследования является разработка математической модели, алгоритма и программного комплекса определения оптимальных значений проектных параметров стальных портальных рам с элементами переменного сечения при выполнении требований реального проектирования.
Для достижения этой цели были решены следующие задачи: - разработан алгоритм поиска оптимальных по критерию минимума массы конструкции значений проектных параметров стальных портальных рам с элементами переменного сечения;
6
- на основе метода конечных элементов реализован алгоритм статического расчета рамных металлоконструкций с элементами переменной жесткости с учетом геометрической нелинейности;
- разработан алгоритм учета ограничений типа неравенств, используемый в контексте генетического алгоритма;
- проведены численные эксперименты с целью проверки применимости разработанных моделей и алгоритмов.
Научную новизну работы составляют:
- Алгоритм оптимального проектирования стальных портальных рам с элементами переменной жесткости, разработанный на основе генетического алгоритма.
- Методика определения верхнего предела минимальной критической нагрузки потери устойчивости рамы, полученная на основе аналитических преобразований обобщенной матрицы жесткости рамы.
- Программный комплекс оптимального проектирования стальных портальных рам с элементами переменной жесткости, разработанный на основе предложенного расчетного аппарата.
- Алгоритм учета ограничений типа неравенств, используемый в контексте генетического алгоритма и основанный на разделении пространства случайных событий, соответствующих выбору допустимых и недопустимых решений, без привлечения метода штрафных функций.
На защиту выноситься:
- Математическая модель и алгоритм оптимального проектирования стальных портальных рам с элементами переменного сечения.
- Программный комплекс для расчета и проектирования стальных портальных рам оптимальных по критерию минимальной массы конструкции.
- Теоретические предпосылки и расчетный аппарат, используемые для поиска оптимальных значений проектных параметров.
- Алгоритм учета ограничений типа неравенств, используемый в контексте генетического алгоритма и основанный на разделении пространства случайных
7 событий, соответствующих выбору допустимых и недопустимых решений, без привлечения метода штрафных функций.
5. Результаты численного исследования напряженно-деформированного состояния стальных портальных рам с элементами переменной жесткости.
8
Глава 1. ОБЗОР МЕТОДОВ РАСЧЕТА И ОПТИМАЛЬНОГО ПРОЕКТИРОВАНИЯ РАМНЫХ МЕТАЛЛОКОНСТРУКЦИЙ
1.1. Обзор методов расчета рамных металлоконструкций
Металлические конструкции характеризуются надежностью работы при различных видах напряженного состояния, обладают высокой несущей способностью при сравнительно небольшой собственной массе [32, 79].
Работы В.Б. Мазура [64] и А.Е. Евсеева [34] посвящены численному исследованию работы под нагрузкой отдельных тонкостенных стержней открытого профиля и конструкций, состоящих из таких стержней. В данных работах шагово-итерационные исследования методом Ньютона-Рафсона основаны на предпосылке о недеформируемости контура поперечного сечения. Поэтому выявление резервов несущей способности этими методиками не является достаточно обоснованным. Более точный расчет может основываться на моделировании тонкостенных стержней открытого профиля, например, пластинчатыми или объемными элементами. Так, в работе [125] представлена конечно-элементная модель стержней двутаврового сечения с применением плоских конечных элементов для оценки величины нагрузки, соответствующей потери устойчивости. Такая модель позволяет отказаться от предпосылки о недеформируемости контура сечения. Однако такой подход может потребовать значительных вычислительных затрат и может использоваться для исследования и прогнозирования несущей способности отдельных конструкций, в то время как алгоритмы глобального поиска, характерной чертой которых является исследование всего пространства возможных решений, могут требовать до нескольких сотен тысяч и более исследований различных, решений. Вместе с тем, соблюдение требований нормативных документов в отношении устойчивости поясных листов и стенок позволяет при проектировании новых сооружений включать такие стержни в расчетную схему как стержневые элементы.
В работах А.Е. Евсеева [34] и Д.А. Казакова [45] для исследования несущей способности стержневых конструкций с учетом их физико-механических характеристик, начальных и приобретенных несовершенств принимается
9
неизменным положение центров тяжести приведенных поперечных сечений, что является источником погрешности расчета даже конструкций из стержней пучкового профиля.
Монография Е.П. Попова "Теория и расчет гибких упругих стержней" [85] посвящена изложению нелинейной теории больших перемещений при плоском изгибе упругих стержней, основанной на точном решении дифференциального уравнения упругой оси стержня. На основе этой теории разрабатываются три метода исследования и расчета тонких упругих стержней: метод эллиптических параметров с использованием числовых таблиц, метод упругих параметров с использованием специальных диаграмм и метод численного решения на ЭВМ. Задачи об упругом изгибе стержня при больших перемещениях условно разделены на три класса:: 1) задачи основного класса; 2) задачи, сводящиеся к основному классу; 3) задачи, не сводящиеся к основному классу. К основному классу относятся задачи, характеризующиеся следующими признаками: 1) начальная кривизна продольной оси стержня постоянна; 2) изгибная жесткость постоянна; 3) изгиб стержня происходит только под действием сосредоточенных сил и изгибающих моментов, приложенных по концам стержня. Случай переменного поперечного сечения относится к классу задач, не сводящихся к основному. Данные условия делают необходимой дополнительную дискретизацию при наличии стержней переменной жесткости, причем отсутствует четкий критерий оценки погрешности при недостаточно подробной дискретизации.
Одним из эффективных путей создания экономичных стальных конструкций является использование пластического резерва несущей способности. Основу методов расчета с учетом пластических свойств материалов составили фундаментальные работы А.А. Гвоздева, В.М. Келдыша, Н.И. Безухова, И.И. Гольденблата, В.В. Соколовского, А.Р. Ржаницына, Л.М. Качанова, А.А. Чираса и других ученых-исследователей, также зарубежных: Ф. Блейха, В. Койтера, Е. Мелана, В. Прагера, Ф. Ходжа и других.
Основой практических методов расчета изгибаемых конструкций, работающих за пределом упругости, является техническая теория изгиба стержней в физически нелинейной постановке. В работе [97] СЮ. Саврасов для исследования упруго-
10
пластических состояний стальных балок использует диаграмму Прандтля и разрабатывает соответствующие аналитические выражения для практических расчетов балок двутаврового сечения. Разработке аналитических решений задач упруго пластического расчета бистальных изгибаемых стержней при кусочно-линейной аппроксимации диаграммы (а, є ) посвящена работа [42] П.С. Иванова.
До создания эффективных алгоритмов расчета с учетом физической и геометрической нелинейности получил широкое распространение метод предельного равновесия, или, применительно к расчету рам, метод последовательного образования пластических шарниров вплоть до перехода стержневой системы в механизм. Вопросы использования этого метода для расчета рам на однократное и повторно-переменное нагружение рассматриваются, например, в работах [26, 60, 94, 115]. Механизм разрушения рамы представляется как кинематическая цепь, состоящая из стержней расчетной схемы, соединенных шарнирами в местах образования пластических шарниров. Основными недостатками метода последовательного образования пластических шарниров являются следующие [26, 96, 63]:
- Для большинства рам предельные значения нагрузок по устойчивости конструкции не позволяют принимать тот или иной механизм разрушения. Такие конструкции при разрушении являются статически неопределимыми.
- Идеализированное представление упруго-пластического состояния элементов конструкции и процесса перехода конструкции в это состояние.
Наиболее приемлемы для реализации на ЭВМ алгоритмы определения упруго-пластических состояний, основанные на последовательных приближениях. Например, в работе [54] преложен метод быстрого спуска, который позволяет, с помощью последовательных приближений получить сколь угодно точные значения относительного удлинения и кривизны оси стержня в любой точке пространства внешних нагрузок.
Выбор закона деформирования материала, устанавливающего связь между напряжениями и деформациями в конструкции, должен отвечать наблюдаемым экспериментально механическим свойствам материала и условиям работы конструкции. Вместе с тем, общепринята применимость линейной модели работы
11
стальных конструкций. Применение расчетных моделей, учитывающих работу материала в неупругой области, связано с обеспечением надежности конструкции в условиях повторно-переменного нафужения [91, 43, 117, 119, 62] и другими факторами, учет которых может потребовать применение упругой модели [96, 13].
Исследование геометрической и физической нелинейности повышает точность моделей строительной механики, расширяет возможности исследования напряженно-деформированного состояния и поведения конструкции под нафузкой по сравнению с линейной теорией. Нелинейная теория позволяет рассчитывать и изучать процессы деформирования конструкций в упругопластической стадии работы материала [68,15, 2].
Для расчета стержневых металлоконструкций с учетом физической и геометрической нелинейностей могут использоваться [40] прямой итерационный метод и шагово-итерационный метод. Решение шагово-итерационным методом является более точным, так как необходимость шагового приложения нафузки обусловлена предпосылкой о малости деформаций, лежащей в основе применяемых методов расчета (метод перемещений и другие).
В работах [83, 41, 84] разрабатывается метод расчета плоских стержневых систем с учетом геометрической нелинейности. Причем, в противоположность принятию некоторой достаточно подробной дискретизации и вычисления соответствующих компонентов вектора невязки усилий [135, 138, 127, 139, 130, 114], устанавливается связь между усилиями по концам элемента, находящегося в деформированном состоянии. В работах [37, 36, 52, 73] для определения напряженно-деформированного состояния геомефичеки и физически нелинейных просфанственных рам используется принцип возможных перемещений. Приложение динамического профаммирования к решению задач расчета упругих стержней постоянной и переменной жесткости с учетом геометрической нелинейности рассматривается в работе [89].
12 1.2. Обзор методов оптимизации рамных металлоконструкций
Задача определения оптимального по некоторому критерию проектного решения может быть сформулирована при наличии непустого множества возможных решений. Вариантов может быть конечное число (задачи дискретной оптимизации), однако большинство практических задач оптимизации конструкций характеризуются столь большим пространством возможных решений, что метод полного перебора решений, гарантирующий отыскание глобального оптимума, в настоящее время неприемлем для решения этих задач, а локальные минимумы могут сильно отличаться от глобального и давать значительно менее рациональные решения [82,95, 96,25].
Для математической формулировки задачи оптимизации необходима формализация критерия эффективности (например, вес конструкции, затраты на ее создание) того или иного приемлемого решения и задание способа расчета на соответствие наложенным ограничениям. Первые математические формулировки задач, связанных с оптимальным проектированием конструкций, даются в трудах Галилео Галилея и Лагранжа. Основы современной теории оптимального проектирования, характеризующейся широким применением вычислительной техники, заложены в работах И.М» Рабиновича, К.М. Хуберяна, К.Г. Протасова, Ю.А. Радцига, А.И. Виноградова, А.А. Чираса и других ученых.
Достижения в области электронной вычислительной техники вместе с развитием теории оптимального проектирования обеспечили возможность эффективного решения более широкого круга практических задач оптимального проектирования конструкций в сравнении с применением только аналитических решений. Математическое программирование, возникшее в конце 30-х годов ХХ-го века, получило признание в ряде прикладных областей, связанных с поиском оптимальных решений. Использование идей математического программирования, как правило, позволяет формализовать и упорядочить постановку и пути решения различных задач [116]. Разработанные методы математического программирования могут быть разделены на методы регулярного (детерминированного) поиска, методы случайного поиска, а также методы, комбинирующие случайный и детерминированный поиск [95].
13
Развитие теории оптимального проектирования с середины ХХ-го века связано с применением электронной вычислительной техники и вместе с математическим программированием привело к переоценке методов оптимизации, применявшихся ранее и основанных на использовании классического анализа. Однако на протяжении десятилетий из известных классов задач математического программирования лишь задачи выпуклой оптимизации могли решаться сколько-нибудь эффективно [9,96, 72].
Основной особенностью поиска оптимальных проектных решений статически неопределимых конструкций является зависимость напряженно-деформированного состояния от распределения жесткостей по элементам конструкции. Кроме того, при постановке задач оптимального проектирования конструкций исследователи стремятся, по возможности, свести к минимуму идеализацию и максимально приблизить расчетную модель к действительности [99]. Учет ограничений реального проектирования часто значительно повышает сложность формулировки задач оптимизации [96].
Одним из предложенных подходов к решению задач оптимального проектирования строительных конструкций является разделение задачи на ряд задач меньшей размерности и переход к поэтапной оптимизации с применением итерационных алгоритмов [25, 1]. А именно, в некоторых случаях большого количества проектных параметров применяют декомпозицию — расчленение исходной задачи на ряд отдельных, и агрегирование — замену какой-либо группы переменных, характеризующих состояние системы, одной переменной. Результатом является иерархическая система задач оптимизации, количество варьируемых переменных на каждом этапе резко сокращается. В этой системе решение исходной задачи зависит от нескольких частных, подчиненных ей задач второго уровня иерархии, каждая из которых зависит от нескольких задач третьего уровня, и так далее. Такое разделение на отдельные подзадачи возможно лишь условно за счет разумного пренебрежения некоторыми связями между ними. Разделение исходной задачи вносит погрешности, часто существенные [25, 1, 44, 61].
Работа [3] В.Н. Алехина посвящена разработке на основе уточненной расчетной модели эффективной методики оптимального проектирования стальных
14
многоэтажных рам с учетом развития пластических деформаций в узлах. Учет конечной жесткости узлов в расчетной схеме рамы выполняется на основе установленной зависимости между жесткостными параметрами стержневой вставки, аппроксимирующей узловое соединение, и сечений элементов, входящих в узел. Отмечаются два направления в оптимальном проектировании конструкций. Первое направление базируется на прямом оптимизационном расчете, который заключается в выборе таких значений проектных параметров, при которых максимизируется принятый показатель оптимальности и удовлетворяются все наложенные требования. Второе направление основывается на серии итерационных расчетов системы при предварительном назначении геометрических параметров и материала элементов конструкции (начальные условия), затем находится напряженно-деформированное состояние конструкции, по которому корректируются начальные условия. На каждой итерации при корректировке начальных условий значение целевой функции изменяется в соответствии с принятым критерием оптимальности. В работе делается вывод о преимуществе второго направления для решения задач оптимального проектирования сложных многопараметрических рамных систем с учетом реальных проектных ограничений.
Двухэтапный подход к оптимизации стержневых систем предлагается в работе [120] Е.В. Янькова. На первом этапе проводится исследование пространства возможных решений для получения начального решения для этапа локального поиска. При поиске решения задачи математического программирования ограничения включаются в целевую функцию с использованием метода штрафных функций (выбор вида штрафных функций и значений параметров этих функций может оказывать сильное влияние на результат решения задач оптимального проектирования конструкций [47]). Примеры использования метода поэтапного решения задачи оптимального проектирования конструкций содержатся также в работах [ПО, 109]. В работе [28] рассматривается поэтапный подход, при котором задачи оптимизации отдельных узлов и примыкающих к ним элементов с учетом ограничений по несущей способности выделены в первый этап на каждой итерации. На втором этапе решается задача оптимизации для всей конструкции в
15
редуцированном пространстве проектных переменных с учетом всей системы наложенных ограничений.
В статье [108] оптимизационный расчет стержневых металлических конструкций предлагается представить в виде совокупности (трех) этапов, на каждом из которых решается задача или последовательность задач линейного программирования. На первом этапе решается задача поиска оптимальной конструкции без учета ограничений по деформациям. В результате определяются нижние пределы площадей сечений элементов и усилия предварительного напряжения. - На втором этапе решается задача минимизации стоимости (массы, объема материала) конструкции при ограничениях по величине деформаций. На третьем этапе расчета определяется максимальная несущая способность конструкции с заданными сечениями элементов. В результате определяются новые усилия предварительного напряжения и новые нижние пределы площадей сечений элементов, используемые в качестве исходных для дальнейшего расчета. Расчет повторяется до достижения удовлетворительного совпадения результатов предыдущего и последующего циклов.
Оптимизация сечений отдельных элементов ведет к существенному снижению расхода материала на сооружение [76]. Задача определения оптимальных параметров сечения отдельных элементов системы должна быть составной частью задачи оптимального проектирования сооружений в целом. В статье [76] предлагается алгоритм автоматизированного подбора сечения стальных составных ригелей, реализующий итерационный процесс поиска оптимальных параметров симметричных двутавровых сечений по одному независимому варьируемому параметру — гибкости стенки. В работе [98] для оптимизации сечений стержней по критерию минимума площади при удовлетворении конструктивным ограничениям, условиям прочности и жесткости используется метод покоординатного спуска (восхождения).
Часто задачи оптимального проектирования конструкций характеризуются нелинейностью целевой функции, наличием некоторого множества локальных экстремумов и необходимостью применения итерационных методов решения. В таких задачах для определения наиболее рационального решения может
16
потребоваться применение методов многоэкстремальной оптимизации, характерной чертой которых является исследование области допустимых решений [81, 63]. В. Прагер в работе [92] подчеркивает необходимость применения эффективных численных методов, так как во всех случаях, исключая самые простые, нелинейный характер критериев оптимальности делает аналитические методы практически непригодными.
В работах [57, 56, 38] задачи оптимального проектирования решаются использованием аналитических преобразований. Решение задач оптимизации, которые, по-видимому, не имеют простых аналитических решений, Л.А. Растригин в [95] разделяет на методы регулярного поиска и методы случайного поиска.
В случае линейной целевой функции и системы ограничений, задаваемых линейными равенствами и неравенствами, имеет место задача линейного программирования. Линейное программирование является: одним из наиболее изученных разделов теории экстремальных задач и может успешно применяться для исследования и анализа широкого класса реальных технико-экономических задач. Первая работа по линейному программированию была опубликована Кантаровичем Л.В. в 1939 году. Симплекс-метод решения задачи линейного программирования сформулировал Дж. Данциг в 1947 году [63, 19].
В задачах линейного программирования понятие угловой точки играет особую роль и лежит в основе многих методов решения таких задач. Для решения задач линейного программирования полный перебор всех угловых точек множества возможных решений практически не применяется, так как даже в задачах не очень большой размерности число угловых точек может быть настолько большим, что простой перебор за разумное количество времени может оказаться невозможным. Тем не менее идея перебора угловых точек послужила основой ряда методов решения задач линейного программирования. Одним из таких методов является так называемый симплекс-метод, позволяющий рассматривать относительно небольшое число угловых точек для определения решения задачи [19, 96, 49, 50].
Идея симплекс-метода состоит в том, чтобы, начав с некоторого начального допустимого базисного решения, переходить от одного такого решения к другому при монотонном улучшении значения показателя эффективности до получения
17 оптимального решения [82, 90, 96]. Задачи линейного программирования используются также и в качестве вспомогательных во многих методах решения нелинейных задач минимизации [19, 96]. Однако линеаризация может сопровождаться потерей точности.
Известно, что в случае статически определимых конструкций, проектируемых без учета нелинейных эффектов, при изменении распределения жесткостей по элементам конструкции повторное определение внутренних усилий не требуется. Один из приближенных методов оптимизации строительных конструкций является подход, заключающийся в том, чтобы выбрать некоторые значения геометрических характеристик, определить усилия в элементах конструкции и использовать результаты для выбора новых значений геометрических характеристик [4, 5]. Полученное таким образом проектное решение может отличаться от наилучшего [63], однако подобные методы поиска могут оказаться наиболее приемлемым для решения задач оптимального проектирования сложных многопараметрических рамных систем [3].
В ряде итерационных методов минимизации функций многих переменных используется совпадение направления наибыстрейшего возрастания функции в некоторой точке с направлением градиента функции в этой точке, а направление наибыстрейшего убывания — с направлением антиградиента [19]. Поиск оптимального решения по методу наискорейшего спуска начинается с некоторого допустимого решения и продолжается в направлении вектор-градиента, который вычисляется не в каждой точке [63, 95, 58]. Основным недостатком метода отыскания экстремума по условию равенства вектора-градиента нулевому вектору при решении задач оптимального проектирования конструкций является: то, что экстремум может быть неаналитическим (находиться на границе допустимой области) [96].
Динамическое программирование связано с разделением процесса проектирования на ряд этапов.. Например, в многоэтажной раме после того как определены значения проектных параметры балок и колонн верхнего этажа определяются значения проектных параметров балок и колонн нижеследующего этажа и так далее до уровня фундамента. Оптимизация проекта проводится на
IS каждом этапе, и при этом окончательный проект является результатом последовательности этих процессов оптимизации [63]. Эффективным может оказаться совместное использование динамического программирования и случайного поиска [10].
Для решения задачи оптимизации методом динамического программирования необходимо соответствие целевой функции принципу аддитивности, то есть возможность представить ее виде суммы функций, каждая из которых выражается через одну переменную. Аппарат динамического программирования применим и в случае непрерывных множеств значений проектных параметров. Решение оказывается приближенным вследствие дискретизации этих множеств [88]. При использовании динамического программирования могут встречаться трудности, заключающиеся в сложности формулировки задач в пригодном для динамического программирования виде [63].
Часто для выбора перспективной начальной точки применяют метод случайного поиска. При генерировании пробных точек желательно равномерное их распределение, поскольку информация о допустимой области и характере целевой функции на этой области отсутствует. Чем равномернее распределены пробные точки в области поиска, тем выше вероятность их попадания в окрестность глобального экстремума [29]. Из всего комплекса качеств, которыми должны обладать алгоритмы многопараметрической оптимизации следует, прежде всего, выделить универсальность и приспособляемость к конкретной математической модели объекта оптимизации. Из методов многопараметрической оптимизации наиболее универсальными являются статистические методы, объединяющие большую группу методов случайного поиска [17].
К настоящему времени методы случайного поиска получили широкое распространение, в особенности при решении многопараметрических задач [16]. Методы случайного поиска, основанные на использовании случайных или псевдослучайных чисел, характеризуются как универсальные [96, 95, 111, 21]. Метод, называемый слепым поиском, заключается в проверке случайных точек области поиска, координаты которых определяются случайными числами, генерируемыми в соответствии с равномерным распределением. Слепой случайный
19 поиск имеет низкую эффективность, но может применяться в сочетании с методами локальной оптимизации для определения начальных точек при решении многоэкстремальных задач. Большие возможности ускорения сходимости алгоритмов случайного поиска заключается в изменении закона распределения генерируемых точек в пространстве возможных решений. Эффективность алгоритма "слепого поиска" резко возрастает, если при оптимизации методом случайного поиска использовать алгоритмы самообучения [33,111]..
Традиционно в задачах оптимального проектирования конструкций формируется некоторая целевая функция вместе с требованием ее минимизации или максимизации в соответствии с выбором того или иного критерия оптимальности конструкции. Критерии, которые могут быть сформулированы в отношении оптимальности строительных конструкций, характеризуются противоречивостью в том смысле, что в пространстве возможных решений, как правило, не удается • получить наилучшее одновременно по всем показателям качества конструкции решение. Вместе с тем, вес металлической конструкции или ее стоимость, как правило, могут служить достаточно полными критериями оптимальности [99, 46, 79].
К числу распространенных подходов получения глобального критерия оптимальности относится подход, заключающийся в свертке локальных критериев. Методы свертки локальных критериев разнообразны и подробно рассматриваются,. например, в работах [82, 27, 112]. В большинстве современных методов поиска оптимального решения предполагается, что оценка его качества и оптимизация проводятся по одному скалярному критерию.
В задачах многокритериальной оптимизации выделяют множество Парето (множество компромиссов, переговорное множество), определяемое как множество, на котором не может быть получено улучшение одновременно по всем локальным критериям. Одним из подходов к решению многокритериальных задач оптимизации состоит в выборе некоторого одного критерия и формулировке на основе прочих критериев дополнительных ограничений задачи оптимизации. Так, среди критериев эффективности строительных конструкций, как правило, есть противоречащие друг другу, и требование, например, минимального расхода материала на конструкцию
20 дополняется требованием некоторых минимально допустимых прочности и жесткости.
В теории оптимального проектирования строительных конструкций нашли применение различные критерии оптимальности конструкций. Одним из наиболее распространенных критериев оптимальности металлических конструкций является критерий минимальной массы. Близким к этому критерию по смыслу является критерий минимума упругой энергии, однако совпадение этих критериев имеет место не всегда, что делает критерий минимума упругой энергии оправданным не во всех случаях [96, 90]. Другим распространенным критерием оптимальности конструкций является критерий минимальной стоимости. В случае учета только стоимости материала конструкции этот критерий тождественен критерию минимального веса. Однако в общем случае критерий минимальной стоимости позволяет учесть затраты на изготовление и другие экономические факторы. Среди прочих критериев оптимальности можно выделить критерий минимума математического ожидания затрат на конструкцию. Для применения этого критерия необходимы надежные статистические данные [112, 16, 1, 96, 90].
Алгоритмы отыскания равнопрочных, равнонапряженных проектных решений является реализацией (не всегда полной) критерия минимума массы материала конструкции. Известно, что требование равнопрочности не всегда тождественно требованию оптимальности [96, 90]. Исследованию условий реализации различных типов проектов равнопрочных сжато-изогнутых плоских линейно-деформируемых рам посвящены работы [67, 66] Мищенко А.В. и Немировского Ю.В. Композитные или слоистые конструкции могут иметь меньшую стоимость по сравнению с однородными. Важной областью применения слоистых рам является решение задачи о реконструкции существующих рамных каркасов зданий, нуждающихся в усилении [66].
В работе [33] рассматриваются задачи оптимального проектирования, решение которых основано на идее равнопрочности (или равноустойчивости) и сводится к решению дифференциальных и алгебраических уравнений. Метод заданных напряжений, разработанный И.М. Рабиновичем в 1933 г., может быть использован для целенаправленного перебора статически неопределимых систем. Для
21 стержневых конструкций показано, что метод заданных напряжений не гарантирует отыскания оптимальной конструкции. Рассматриваются также задачи линейного программирования (задача оптимизации веса фермы), нелинейного программирования и динамического программирования.
Преобладающее большинство исследований связано с определением параметров поперечных сечений, значительно меньше исследований связано с определением геометрии всей системы [16]. Целевая функция и ограничения часто являются нелинейными, невыпуклыми. В таких случаях целевая функция имеет на множестве допустимых решений несколько локальных экстремумов. Применение методов случайного поиска в ряде таких задач дает возможность построить весьма простые и; эффективные алгоритмы оптимизации, которые по определенным критериям превосходят алгоритмы, основанные на регулярных методах поиска [33, 95].
Требования унификации и стандартизации в прикладных задачах проектирования, как правило, делают необходимой принадлежность искомых значений проектных параметров некоторым множествам дискретных значений, определяемых ГОСТами и сортаментами. Получение решений, соответствующих непрерывным множествам значений проектных параметров, с последующим округлением значений проектных параметров до дискретных значений может приводить к значительно менее рациональным решениям по сравнению с решениями, полученными с учетом дискретности указанных множеств [48,39, 96].
Линейные модулярные формы были предложены Ю.А. Радцигом [93] для оптимизации ферм, но имеются работы по использованию подхода для оптимизации рамных систем [113]. Использование численных методов оптимизации (линейное, нелинейное и динамическое программирование, случайный поиск и другие) позволяет определять эффективные проектные решения в случае задач, не имеющих достаточно простых аналитических решений [96].
Задача оптимизации статически неопределимых систем является в общем случае многоэкстремальной [25, 30, 20]. В статьях отмечается необходимость решения задачи об отыскании оптимальных проектных решений сложных статически неопределимых конструкций с использованием итерационных
22 алгоритмов. В [30, 20] рассматривается один из упрощенных подходов к построению алгоритма оптимизации конструкций, суть которого заключается в следующем. Принимается некоторая начальная точка в пространстве возможных решений и определяются соответствующие характеристики состояния элементов конструкций. Принимая вычисленные значения усилий неизменными, решается задача оптимизации на данном этапе итераций. Полученные значения проектных параметров являются исходными для следующего этапа итерационного поиска. Результаты поиска могут значительно отличаться от испытания к испытанию, но позволяют получить решения, значительно улучшающие исходный проект.
В статье [78] Ольков Я.И. и Антипин А.А. рассматривают задачу об оптимальном распределении материала статически неопределимых шарнирно-стержневых систем при учете ограничений реального проектирования. Для решения предложен итерационный алгоритм, в котором производятся последовательные расчеты системы до сходимости по объему без учета дискретности сортамента. По найденным площадям сечений стержней путем перебора подбираются площади из заданных сортаментов. При поиске из различных начальных точек получаются разные решения.
Искомое решение должно удовлетворять значительному количеству ограничений, среди которых ограничения по прочности отдельных сечений, по общей и местной устойчивости конструкции в целом и отдельных ее элементов. При этом необходимость линеаризации задачи в условиях применения электронной вычислительной техники трудно считать оправданной [25]. Так, решение задач оптимизации конструкций, рассчитываемых на основе метода предельного равновесия, когда расчетная модель принимается жестко-пластической, может быть получено для достаточно сложных рам, плит и других конструкций [94, 60]. Однако столь упрощенная расчетная модель достаточно хорошо описывает действительную работу сравнительно ограниченного круга конструкций, например, таких как стержневые железобетонные системы со стержнями небольшой гибкости, исчерпание несущей способности которых происходит в результате прочностных разрушений.
23
Применение балок с перфорированными стенками, изготовленных из прокатных профилей, на 25-30% экономит расход металла и на 15-20% снижает стоимость. Для решения задачи оптимального проектирования стальных балок с перфорированной стенкой в работе [75] применен метод сканирования по неравномерной дискретной сетке [35]. В алгоритме после предварительного исследования области возможных решений выполняется уменьшение шага сетки сканирования. Сужение области поиска при одновременном повышении точности последнего позволяет быстро найти искомый вектор оптимальных значений проектных параметров.
Задача оптимизации строительных конструкции не обязательно определяет единственное проектное решение, возможно существование нескольких решений, имеющих равные или достаточно близкие значения показателя оптимальности. Часто оправдано принятие любого проектного решения, значение критерия оптимальности которого не превышает, например, более чем 3% по сравнению с оптимальным. Варианты, удовлетворяющие этому условию, могут затем подвергаться неформальному анализу с помощью, например, метода экспертных оценок. Сравнение оптимальных сечений при проектировании стальных рам с сечениями, принимаемыми проектировщиками без оптимизации показывает, что излишний расход материала достигает 20% [92, 96, 13].
В генетических алгоритмах для сравнения качества решений, удовлетворяющих всем ограничениям задачи оптимизации, как правило, используется некоторая целевая функция, тогда как для оценки качества недопустимых решений нет единой методики. Наиболее простой способ учета недопустимости некоторых решений — исключение таких решений из рассмотрения, однако был предложен ряд иных методов [132], обзору которых посвящены, например, работы [132, 121]. В работе [132] отмечается, что в общем случае функции приспособленности допустимых и недопустимых решений различны, подчеркивается наличие следующих вопросов:
- следует ли исключать из рассмотрения недопустимые решения, или, наоборот, рассматривать их способствующими возможности пересекать области недопустимых решений для достижения точки оптимума;
24
- следует ли принимать справедливым, что любое допустимое решение лучше любого недопустимого решения;
- как сравнивать два недопустимых решения;
- следует ли "ремонтировать" недопустимые решения, "перемещая" их к ближайшей точке области допустимых решений, следует ли использовать, эту процедуру для замены решения, или только для вычисления значения функции приспособленности этого решения;
- следует ли использовать штрафные функции.
Метод исключения недопустимых решений из рассмотрения является приемлемым в случае выпуклого множества допустимых решений, занимающего значительную часть всей области возможных решений [132]. В случае малого отношения размера области допустимых решений к размеру области возможных решений значительно более эффективными являются другие методы (например, рассматриваемые в работах [132,121]).
Использование "ремонта" недопустимых решений особенно популярно при решении комбинаторных задач оптимизации, в которых эта процедура является относительно простой. Решение, принадлежащее области допустимых решений, поставленное в соответствие данному недопустимому решению используется для вычисления значения функции приспособленности данного решения, а также для замены (с заданной вероятностью) этого решения [132].
В работе [121] приводится следующая классификация подходов к учету недопустимости некоторых решений:
- использование штрафных функций;
- поддержка популяции допустимых решений, обеспечиваемая специальными операторами эволюционных алгоритмов;
- смешанные методы;
- другие методы.
В работах [128, 51, 126, 124, 132, 121] отмечается, что использование генетических алгоритмов позволяет определять оптимальное решение (некоторых задач оптимизации) или решение близкое к оптимальному. Имеются исследования
25 [например, 128], направленные на выработку и обоснование критериев сходимости генетического алгоритма к глобальному оптимуму.
Использованием профилированного настила вместе с эффективным утеплителем и соответствующим снижением постоянной нагрузки на покрытие созданы предпосылки для широкого применения сплошностенчатых балочных элементов в несущих конструкциях каркасов одноэтажных зданий пролетом ІБ-^ЗО м. Известно, что балочные конструкции обладают рядом преимуществ по сравнению с решетчатыми, а именно: в меньшей степени склонны к хрупким разрушениям, технологичны, просты в изготовлении и монтаже, малоэлементны, имеют большой коэффициент загрузки транспортных средств. Кроме того, решающее значение могут иметь эксплуатационные расходы на создаваемое здание, а не только стоимость создания конструкций. Так, увеличение объема здания за счет высоты ферм покрытия потребуют дополнительных затрат по сравнению с балочными конструкциями. В то же время традиционные решения каркасов зданий из балочных элементов уступают по расходу стали решетчатым конструкциям [100, 1]. Несущая способность неразрезных балок с перфорированной стенкой превышает несущую способность разрезных балках в упругой стадии работы в среднем на 8.5%. Регулирование напряжений позволяет удлинить область упругой работы до 8% и более по сравнению с неразрезными моделями без регулирования напряжений [12].
Портальные рамы с шарнирным опиранием колонн на фундамент представляют собой один из основных типов решения поперечной рамы одноэтажных промышленных зданий. Когда необходимо иметь небольшую строительную высоту, обычно используются сечения ригеля и колонн в виде сварного двутавра, что значительно снижает трудоемкость изготовления и монтажа конструкций. Жесткое соединение ригеля с колоннами позволяет уменьшить изгибающий момент в ригеле, а шарнирное соединение колонн с фундаментом делает систему малочувствительной к неравномерной осадке опор. Двухшарнирные рамы со сплошностенчатыми элементами ригеля и колонн применяются при длине пролета до 60 м [65, 13].
В ЦНИИСК им. В.А. Кучеренко в течение ряда лет проводилась работа по разработке облегченных конструкций, в основу которой был положен принцип
26 достижения наибольшего соответствия между усилиями, возникающими от воздействия внешней нагрузки, и геометрическими характеристиками поперечного сечения по периметру рамы. Жесткое сопряжение ригеля и стоек вместе с шарнирным опиранием стоек на фундаменты дает возможность, наряду с упрощением конструктивного оформления опорной базы стоек, наиболее эффективно использовать переменную высоту сечения по длине элемента в стойках рамы. Рамные конструкции из сварных двутавровых элементов с переменной высотой поперечного сечения позволяют получить экономию стали до 30^-40% по сравнению с конструкциями, в которых элементы ригеля и стоек имеют постоянные поперечные сечения [100,123].
Выводы к главе 1
- Выполненные теоретические и экспериментальные исследования легких металлических конструкций доказывают целесообразность использования в рамных конструкциях стержней переменного сечения.
- Задачи оптимального проектирования строительных конструкций, в которых учитываются требования реального проектирования (требования прочности, устойчивости, дискретности и другие), как правило, являются нелинейными и многоэкстремальными. Проектные решения, соответствующие локальным минимумам могут быть значительно менее рациональными по сравнению с решениями, соответствующими глобальному оптимуму.
- Генетические алгоритмы относятся к алгоритмам глобального поиска и успешно применяются для решения широкого круга задач оптимизации, включая задачи оптимального проектирования строительных конструкций. Использование генетических алгоритмов позволяет определять оптимальные или близкие к оптимальному проектные решения.
- Применение методов оптимизации при проектировании легких металлических конструкций позволяет получать экономию материала до 30% по сравнению с решениями, разрабатываемыми без использования методов оптимизации.
27 5. Разработка новых методов решения задач оптимального проектирования конструкций и исследование применимости существующих методов являются актуальными направлениями в области теории оптимального проектирования.
28
Глава 2. СТАТИЧЕСКИЙ РАСЧЕТ УПРУГОДЕФОРМИРУЕМЫХ СТАЛЬНЫХ ПОРТАЛЬНЫХ РАМ С ЭЛЕМЕНТАМИ ПЕРЕМЕННОЙ ЖЕСТКОСТИ
2.1. Основные предпосылки и допущения. Формирование расчетной схемы рамы
- Рассматриваются симметричные стальные портальные рамы с элементами переменного сечения.
- Элементами рамы принимаются стержни составного двутаврового сечения с переменной высотой стенки. Положение стержневых элементов в расчетной схеме принимается в соответствии с геометрическим местом точек центров тяжести поперечных сечений стержней рамы.
- Элементы рамы проектируются линейно упруго-деформируемыми.
- Расчет производится на действие статической нагрузки. Учет геометрической нелинейности выполняется с использованием метода Ньютона-Рафсона [135, 138, 127,139, 130].
- Общая устойчивость рамы оценивается сравнением величины нагрузки на раму с величиной минимальной критической нагрузки потери устойчивости рамы, расчетом с учетом геометрической нелинейности и требованиями устойчивости отдельных элементов по методике норм проектирования [105].
- Учет эксцентричности соединения элементов рамы осуществляется включением в расчетную схему соответствующих абсолютно жестких вставок в плоскости стыка элементов.
Рассматриваем симметричные стальные портальные рамы, схематически показанные на рис. 2.1. Задачу оптимизации определяем как отыскание таких значений \хих2,...х^}т (где Nd— количество проектных параметров), чтобы вес портальной рамы был минимальным при выполнении ограничений по состоянию конструкции g,(x)<0 (неравенства определяются требованиями по прочности, жесткости, местной и общей устойчивости). Для определения оптимального решения в рамках исследуемой модели стальной портальной рамы рассматриваем четыре конструктивные варианта. Это варианты с четырех- и шести-стержневым симметричным ригелем. Принятие центральных фрагментов ригеля в виде стержней
29
с перфорированной стенкой образует соответствующие дополнительные два варианта конструктивного решения рамы.

| Х\ | ||||
| (xi+X\X2)/2 | ||||
| Х4 | Х\Х2 | |||
| \ | ||||
| В '1 А | 1 1 1 1 / 1 | 1 | ||
| (хі-л:ід:2)/2 | ||||
'\
U1
1-1
Хг
х5
Рис. 2.1. Схемы рам и отдельного стержня рамы с обозначениями проектных параметров.
Заданными параметрами оптимизации, кроме варианта проектного решения, принимаем: высоту Я, рамы в верхней точке внешнего периметра; высоту Я2 внешней грани колонны; длину L пролета рамы; пределы интервала или дискретное множество возможных значений каждого проектного параметра; модуль упругости Е; расчетное сопротивление по пределу текучести Ry; расчетное сопротивление по временному сопротивлению Ru.
Стержни рамы принимаем симметричного двутаврового сечения переменной высоты по длине стержня. Положение стержневых элементов в расчетной схеме принимаем в соответствии с геометрическим местом точек центров тяжести поперечных сечений стержней рамы. Возможные эксцентриситеты учитываем включением абсолютно жестких вставок между точками пересечения центральных осей смежных стержней с плоскостью стыка этих стержней.
30
В качестве независимых проектных параметров х, принимаем параметры, определяющие: размеры элементов поперечных сечений стержней рамы, линейное изменение высоты поперечного сечения каждого стержня рамы, координаты точек пересечения проекций плоскостей стыка фрагментов ригеля с внешним периметром рамы.
Точки внешнего контура рамы определяются заданными параметрами и проектными параметрами, определяющими координаты точек стыка элементов ригеля. В качестве плоскости стыка смежных элементов принимается плоскость, проходящая через вершину угла внешнего контура, разделяя его пополам.
Закон линейного изменения высоты поперечного сечения стержня рамы определяем двумя проектными параметрами этого стержня (х, и х2 на рис. 2.1). Это параметры, определяющие условную высоту поперечного сечения стержня и положение внутренней грани элемента рамы. Все проектные параметры центральных фрагментов ригеля принимаем независимыми, для остальных стержней рамы независимыми параметрами принимаем все за исключением параметров, определяющих условную высоту поперечного сечения этого стержня. Значение этих параметров определяем из условия совпадения с заданной точностью точек пересечения внутренних граней смежных элементов с плоскостью стыка этих элементов.
Таким образом, заданные параметры вместе с проектными параметрами полностью определяют расчетную схему. Далее рассмотрим определение геометрических характеристик стержней портальной рамы в соответствии с принятой моделью рамы на примере стержня колонны и стержня ригеля с перфорированной стенкой.
Площадь поперечного сечения колонны в произвольной точке z отрезка СХС2 может быть вычислена по формуле:
А(2)=2х3^- + х,-(н(г)-^±-\ (2.1)
cosa \ cosa)
где х,-— проектные параметры (см. рис. 2.1);
cosa - косинус угла между центральной осью стержня и поясными листами, вычисляемый по формуле:
31
X\X2
cosa =
т]н22+(ххх2У
где x,, x2 - проектные параметры (см. рис. 2.1); Нг — длина внешней грани АВ колонны; H(z) - высота сечения колонны в точке z:
'Н.-Н^
H(z)= H0 +
I
где / - длина отрезка СХС2 оси стержня-колонны;
Н0, Н, - высота поперечного сечения колонны, соответственно, в точках Сх и С2 (рис. 2.1):
\е-АСх
е-ВС,
Я0=-
•2,
2; я,=
сауа cosa
где cosa - тоже,что ив (2.1);
е — единичный вектор, перпендикулярный вектору АВ внешней грани стержня колонны:
| -(ав\ (ав)х |
| АВ АВ |
где \АВ)Х, \АВ)у - проекции вектора АВ на оси общей системы координат (см. рис.
2.1); Момент инерции поперечного сечения колонны в произвольной точке z отрезка СХС2 вычисляем по формуле:
7(z)=2| ^-f-^i-T +J^.(o.5H(z)-^)2 ) + L.f#(z)--^±-T (2.2)
I \2\cosaJ cosa у cosaj I 12 ^ cosa)
где xt - проектные параметры (см. рис. 2.2);
cosa - тоже, что и в (2.1); H(z) - тоже, что и в (2.1).
Площадь поперечного сечения в произвольной точке z отрезка С5С6 участка
ригеля с перфорированной стенкой с учетом отверстия вычисляем по формуле (см.
рис. 2.3):
4»=2xI4-*i- + *I6 {H(z)-^--xl2xiX (2.3)
cosa \ cosa J
где х, - проектные параметры (см. рис. 2.3);
32
*12*13
cos a - косинус угла между поясными листами и осью стержня, вычисляемый по формуле: cosa =
DE
где хп, х13 - проектные параметры (см. рис. 2.3); - длина внешней грани DE стержня;
H(z) - высота поперечного сечения ригеля в точке z отрезка С5С6:
Я (z)= Я0 +
Н1~Н0
I
z,
где / - длина отрезка С5С6 оси стержня;
Н0, Н, - высота поперечного ригеля в точках С5 и С6, соответственно:
е-ЕС
е-DC,
Н0 =
•2; #,=
cosa cosa
где cosa - то же, что и в (2.3).
е - единичный вектор, перпендикулярный вектору DE внешней грани фрагмента ригеля:
DE
\DE\
DE\
где \DE)X, [DE)y — проекции вектора DE на оси общей системы координат (см.
рис. 2.1);
33
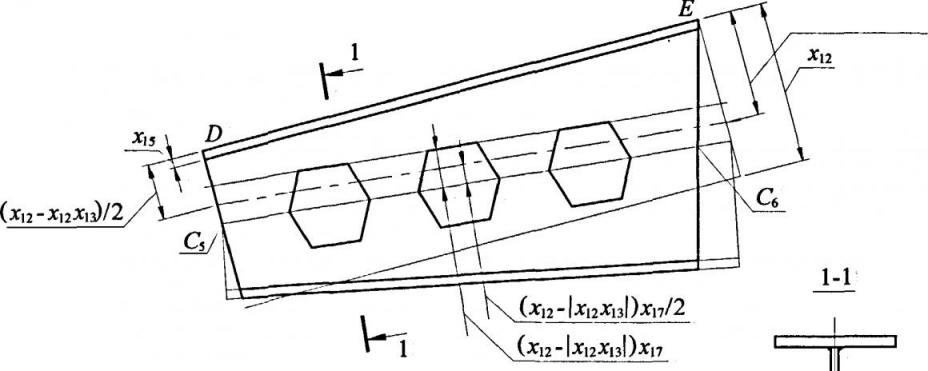
(хі2+х12Хіз)/2
і *іб
•*14
Рис. 2.2. Основные проектные параметры фрагмента ригеля с перфорированной стенкой.
Момент инерции поперечного сечения в произвольной точке z отрезка С5С6 участка ригеля с перфорированной стенкой с учетом отверстия вычисляем по
формуле (см. рис. 2.3):
ill 12
ґН(г) 0.5х15 2 cos a
Х<лХ,
,2\
'(0=2
44
45
12
14А15
\cosaj cosa где х, — проектные параметры (см. рис. 2.2); H(z) — то же, что и в (2.3); cosa — то же, что и в (2.3).
Ґ 2х V
Н&-^ -ТТ-^иУ (2-4) cosaj 12
2.2. Вычисление элементов матрицы жесткости стержня переменного сечения
Формирование матриц жесткости стержней расчетной схемы является необходимой частью статического расчета методом перемещений. Элементы матрицы жесткости стержневого элемента переменного сечения могут быть вычислены с учетом сдвиговых деформаций [118] или с учетом только изгибной податливости. В данном разделе рассмотрим формирование матриц жесткости без учета сдвиговых деформаций с использованием численного интегрирования,
34
линейной аппроксимации и степенной функции. Проведем сравнение эффективности применения этих методов в алгоритме расчета с учетом геометрической нелинейности, когда требуется вычисление матриц жесткости для большого количества стержневых конечных элементов.
Для вычисления элементов матриц жесткости отдельного стержневого элемента необходимо вычисление следующих интегралов [118, 133]:
' 1 ' 1 ' ' 2
[ —dz. | dz, Г dz, Г——dz, (2.5)
lEA{z) 'iEI(z) lEI(z) JEI(z)
где EA{z) - закон изменения продольной жесткости по длине стержня;
El(z) — закон изменения изгибной жесткости по длине стержня;
/ - длина стержня.
2.2.1. Применение численного интегрирования. Линейная аппроксимация функции изменения жесткости стержня.
Численное интегрирование* выражений (2.5) выполняется применением формулы прямоугольников, формулы трапеций, формулы парабол (Симпсона), формулы Чебышева, формулы Гаусса. Точность названных формул, как правило, возрастает при увеличении количества отрезков между пределами интегрирования. Значения определенных интегралов, полученные численным интегрированием и используемые для формирования матрицы жесткости стержня переменного сечения, П.П. Шандрук в работе [118] характеризует как точные.
В случае линейного изменения жесткости продольного деформирования и жесткости на изгиб интегралы (2.4) могут быть вычислены непосредственно с получением соответствующих аналитических выражений:
1, ln(A0+kAz)'
(2.6)
f l- dz=-
>E(A0+kAz) kAE
1 ln(I0+k,z)
(2.7)
f i dz =
о
lE(I0 + klZ) k,E
* Яковлев К.П., Лунц Г.Л., Янпольский А.Р. Численное интегрирование (механические квадратуры) //С.207-210 в книге: Яковлев К.П. Краткий физико-технический справочник, Т.1, — М.: Физматгиз, 1960. - 447 с.
35
\ dz J— fy-HL+k.z)
(2.8)
( 22 Z-I Iі
l 2
(2.9)
f—Z- dz =
\lk,E k)E k)E
где кА=(А1-А0)-Г\ ^(Wo)-/-1.
2.2.2. Использование степенной функции.
Кроме численного интегрирования и интегрирования выражений (2.5) принимая линейное изменение, функция изменения продольной и (или) изгибной жесткости может быть принята в виде степенной функции
EI(z) = EI0
1-
ч:
(2.10)
где /0, /, — значение момента инерции концевых сечений стержня.
Данная функция имеет преимущество применения линейной аппроксимации, такое как интегрируемость в элементарных функциях:
Е10 • а • (т -1)
1, -(1 + а-г)1"ж dz=-
z, -(mza + mz2a2 -z2a2 +1),,
!EI(z)
(m-2)(m-Y)a2EI0
dz =—^— — —— (1 + аг)
V z2, -(z2a2(m2 -m) + z3a\m2 -3m + 2) + 2mza + 2) „
I UZ =— -fl — OLZ)
*El(z) EIQa\m3 -6m2+llm-6)
где EI(z) - функция вида (2.10) изменения изгибной жесткости; a = -(l-(l-^[Uh))rl.
Степенная функция (2.10) может иметь более точное соответствие действительному закону изменения значения момента инерции по длине стержня в сравнении с аппроксимацией линейной функцией. Однако итерационное определение значения коэффициента т без гарантии достижения сколь угодно точного соответствия действительному закону изменения жесткости снижает эффективность применения степенной функции (2.10) в сравнении с численным
36
интегрированием. Кроме того, дополнительное разбиение на конечные элементы стержней расчетной схемы, необходимое при расчете с учетом геометрической нелинейности, обуславливает повышение точности аппроксимации закона изменения жесткости стержня переменного сечения кусочно-линейной функцией.
2.3. Моделирование эксцентрично-соединенных стержней при расчете стержневой конструкции методом конечных элементов в форме метода перемещений
В итерационных алгоритмах при варьировании значений параметров величины эксцентриситетов в расчетной схеме могут меняться от значительных до малых величин. В практике инженерных расчетов при необходимости учета эксцентриситетов часто включают в расчетную схему абсолютно жесткие стержни, принимая жесткость таких стержней значительно превышающую жесткость остальных. При использовании этого подхода в компьютерной программе необходим анализ возможных случаев, например, "малых" и "больших" эксцентриситетов; также необходима оценка точности получаемых результатов. Принятие недостаточно большой жесткости предполагает наличие некоторой погрешности, с другой стороны, чрезмерное увеличение жесткости в сочетании с малой длиной элемента может привести к вычислительной потере точности. Рассматриваемые ниже соотношения перемещений концевых сечений эксцентрично-соединенных стержней и усилий по концам стержней основаны на предпосылке о малости деформаций, позволяют исключить из расчетной схемы абсолютно жесткие вставки [69].
Рассмотрим составной стержневой элемент, состоящий из упругого стержневого элемента с примыкающим абсолютно жестким стержнем. Локальную систему координат (СК) составного элемента принимаем совпадающей с локальной СК упругого стержня (рис. 2.3). Определим матрицу жесткости составного элемента, соотношение между деформациями (перемещениями концевых сечений) упругого и составного элемента, соотношение усилий по концам элементов.
37
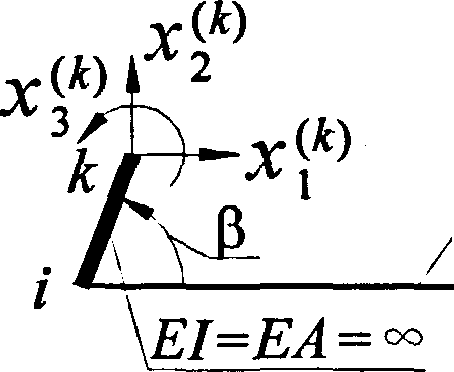
хЬ'У Eli&EALzL xVVL2
^x
J
1
Рис. 2.3. Схема составного элемента.
В составном элементе смещения абсолютно жесткого стержня вызывают определенные деформации упругого стержня. Каждая элементарная составляющая деформации (продольные, поперечные и угловые перемещения концевых сечений) вызывает возникновение реакций по концам упругого стержня и соответствующие реакции по концам абсолютно жесткого стержня.
Перемещения сечения i от единичного горизонтального (в локальной СК) смещения сечения к (рис. 2.4):
Мл = Akxl=l,Aix2=Aix3=0. (2.11)
Перемещения сечения I от единичного вертикального смещения сечения к (рис. 2.6):
Aix2 = Akx2=l, Aixl = Aix3 = О. (2.12)
Перемещения сечения i от единичного углового перемещения сечения к (рис. 2.4):
Дй =^з=1» 5*"*i = (Lki • tg ^хз) • cos (p - я/2), ^^(Lb-tgAkJ-smfa-n/l)
при малых Акх3:
Ых1 = Lu sin P • Akx3 = Z* АкхЪ, Ых2 = Z„ (- cos p) • Akxi = -I* • Mxi.
38
A*,i=l-
xW2
V
З'ї \~Y(/)
-0)
\\Мх2=\
4—
-(/)
-*#к'
У
У *!
Az\,=AA;r
^Ї^О')

АА:х3 = 1 Рис. 2.4. Единичные перемещения сечения к составного элемента.
В соотношениях (2.11) и (2.12) деформации абсолютно жесткого стержня исключены. При угловом перемещении узла к функция
№+bb-*g&*J-Lu (2.13)
изменения длины Ьш стержня имеет нулевой предел и нулевую в пределе производную при Акх3 -> 0. Таким образом, для сколь угодно малого є > 0 можно подобрать такую долю нагрузки, что напряжения (при сколь угодно большой условно принятой жесткости) в поперечном сечении абсолютно жесткого стержня от указанного удлинения не будут превышать заданной доли є максимальных напряжений в каком-либо упругом стержне. Следовательно, при бесконечно малых деформациях погрешность отсутствует.
На основе вышеизложенного формируем матричные соотношения между перемещениями концевых сечений составного и упругого элемента:
| ^,1 | 1 0 | *кх1 | ||||
| Д.2 | 0 1 | -if. | 0 | Лкхг | ||
| А*з | 0 0 | 1 | ЛкхЪ | |||
| 4,1 | 4f,i | |||||
| 4',2 | 0 | Е | 4fx2 | |||
| 4Г* | 4fx3 |
= MA-Ak,
(2.14)
39
где Е — единичный квадрант матрицы.
Для определения соотношения усилий по концам составного элемента и упругого стержня рассмотрим равновесие узла / и стержня k-i (рис. 2.5).

1 ~Л'Х? х®
X
(О І
Рис. 2.5. Усилия в узле i составного стержня. Из уравнений равновесия стержня k-i имеем
х| = xj + х\ • 1% - х'2 • 1%, или в матричной форме
х] ~ xi»
Х2 ~х2>
- О
- О
Lbr 1
О
о
Е
= мх-ху.
(2.15)
Последним равенством определяются также усилия по концам составного стержня от воздействия внешней нагрузки на упругий стержень /-/.
Таким образом, матрицу жесткости составного элемента в локальной системе
координат упругого стержня можно представить в следующем виде
(2.16)
Rk4 = Mx.Rt_j -Мй =MX-Ri_j-MTX,
где Rt j — матрица жесткости упругого стержня.
Приведенные выше соотношения относятся к этапу формирования обобщенной матрицы жесткости стержневой расчетной схемы. Рассмотрим случай эксцентричного соединения по обоим концам стержневого элемента. Матрица Мх, входящая в выражение (2.16), принимает следующий вид
40
Mv =
| 1 | 0 | 0 | |||
| 0 | 1 | 0 | 0 | ||
| r(') | -L« | 1 | |||
| 1 | 0 | 0 | |||
| 0 | 0 | 1 | 0 | ||
| tf> | -HP | 1 |
(2.17)
где Мх — матрица преобразования вектора усилий по концам упругого стержня (в локальной СК этого стержня) к вектору усилий по концам составного стержня (в локальной СК упругого стержня); Z(„°, Х(г° - проекции вектора, совпадающего с абсолютно жестким стержнем, примыкающим к узлу /, и имеющего начало в узле i, соответственно на ош хх,х2 локальной СК упругого стержня; L(J\L(Tj) — проекции вектора, совпадающего с абсолютно жестким стержнем, примыкающим к узлу у, и имеющего начало в узле у, соответственно на оси хх,хг локальной СК упругого стержня.
Рассмотрим независимость вычисляемых значений элементов матрицы преобразования от порядка учета концевых эксцентриситетов. Действительно, условно называя абсолютно жесткий стержень, примыкающий к узлу / упругого стержня "левым эксцентриситетом", и абсолютно жесткий стержень, примыкающий к узлу у упруго стержня - "правым эксцентриситетом", имеем, для случая наличия левого эксцентриситета матрицу преобразования Mf вида (2.15). При этом матрица жесткости составного элемента, включающего упругий стержень и левый эксцентриситет, в локальной СК упругого стержня определяется выражением (2.16):
Ry=Mf.Rt_rMr. (2.18)
Матрица преобразования, учитывающая наличие правого эксцентриситета, имеет вид
о
М? =
о
| 1 | 0 0 |
| 0 | 1 0 |
| 4/> | -4Л 1 |
(2.19)
Учитывая наличие правого эксцентриситета, имеем
r2=mT-rx-m?t,
(2.20)
из (2.18) и (2.20):
41
РОССИЙСКАЯ
ОСУДАРСТВЕННАЯ
БИБЛИОТЕКА
к2=м?.му.я,_гмГ-мГ.
(2.21)
Произведение матриц преобразования в выражении (2.21):
| 1 | 0 | 0 | |||
| 0 | 1 | 0 | 0 | Е | |
| f'Mf = | z,(0 | -*? | 1 | • | |
| 0 | Е | 0 | |||
| 1 | 0 | 0 | |||
| 0 | 1 | 0 0 | |||
| 4° | -4° | 1 | |||
| 0 | 1 0 0 0 1 0 | ||||
| #> | -HP 1 | ||||
1 о
о
- 0
- 0
№ 1
(2.22)
«
Равенства, аналогичные равенству (2.22), имеют место при перестановке матриц (мх\м^), также для транспонированных матриц. Таким образом, вычисляемые значения элементов матрицы жесткости эксцентрично соединенного стержневого элемента не зависит от порядка учета эксцентриситетов.
Пользуясь условиями равновесия узла /, изображенного на рис. 2.5, сформулируем матричное определение вектора перемещений концевых сечений упругого стержня по вектору расчетных перемещений концевых сечений составного стержня:
| *; | |
| х'2 | |
| *3 | |
| */ | |
| XJ л2 | |
| Xі |

